Révisions...
65 messages
- Page 2 sur 4 - 1, 2, 3, 4
salut!
y a encore un souci .. :hum:
je révise un peu les équa. ensemblistes , je crois que j'ai un problème avec la résolution algébrique .
souvent , j'utilise des shémas pour trouver les solutions directement, mais ça marche pas toujours et un shéma ne prouve rien !
je me demande donc : quelles sont les étapes à suivre pour les résoudre? une méthode pratique ? des astuces ?
merci
PS: merci legeniedesalpages , j'avais remarqué ta solution pr l'autre question mais c un peu long par rapport à la remarque d'Emdro !
y a encore un souci .. :hum:
je révise un peu les équa. ensemblistes , je crois que j'ai un problème avec la résolution algébrique .
souvent , j'utilise des shémas pour trouver les solutions directement, mais ça marche pas toujours et un shéma ne prouve rien !
je me demande donc : quelles sont les étapes à suivre pour les résoudre? une méthode pratique ? des astuces ?
merci
PS: merci legeniedesalpages , j'avais remarqué ta solution pr l'autre question mais c un peu long par rapport à la remarque d'Emdro !
Non, je ne pense pas qu'il y ait de méthode générale. A part connaitre les règles sur le bout des doigts pour ne pas passer à côté d'une évidence.
Essayer de "factoriser" un maximum peut-être...
Le schéma est souvent une très bonne idée. Si tu y vois quelque chose, cela peut guider tes pas. Mais par exemple pour ton exo de l'autre soir, j'ai regardé, et je suis tombé directo sur la solution. Pas de schéma, pas d'autre essai... Un coup de chance probablement. :id:
Essayer de "factoriser" un maximum peut-être...
Le schéma est souvent une très bonne idée. Si tu y vois quelque chose, cela peut guider tes pas. Mais par exemple pour ton exo de l'autre soir, j'ai regardé, et je suis tombé directo sur la solution. Pas de schéma, pas d'autre essai... Un coup de chance probablement. :id:
oui ,en effet le shéma facilite bcp la tâche , si l'équation est "simple" .
mais j'ai 2 problème avec le schéma :
-parfois je vois les solutions vérifiant l'équation sans être sûre qu'elles sont les seules !
- la rédaction de la solution . suffit-il de vérifier que la solution marche (pr la réciproque) et écrire l'implication directe ?
bon , par exemple avec cet exemple :
)
la CS ici , c'est B inclus dans A .
je ne vois comme solution que A\B ! mais je sais pas sure sachant qu'une équation ensembliste est loin d'avoir une seule solution .
une idée ?
mais j'ai 2 problème avec le schéma :
-parfois je vois les solutions vérifiant l'équation sans être sûre qu'elles sont les seules !
- la rédaction de la solution . suffit-il de vérifier que la solution marche (pr la réciproque) et écrire l'implication directe ?
bon , par exemple avec cet exemple :
la CS ici , c'est B inclus dans A .
je ne vois comme solution que A\B ! mais je sais pas sure sachant qu'une équation ensembliste est loin d'avoir une seule solution .
une idée ?
Je crois que la solution dans le cas général est 
Pour l'analyse, j'ai travaillé bêtement et méthodiquement: en dessinant trois ensembles qui se coupent (A,B et X). Il y a 7 zones. On les étudie une par une.
Si z est dans A mais pas dans B ni dans X. Alors z est dans , donc dans B. C'est absurde. Donc il n'y a personne dans cette zone.
, donc dans B. C'est absurde. Donc il n'y a personne dans cette zone.
Tu pourras de même éliminer les 2 autres zones où on appartient à un seul des trois ensembles, et également celle où on appartient aux trois simultanément.
Bilan. On est toujours dans exactement deux ensembles:
si on est dans A et B, on n'est pas dans X.
Si on est dans X, on est soit dans A, soit dans B.
D'où .
.
Synthèse immédiate. :happy2:
Pour l'analyse, j'ai travaillé bêtement et méthodiquement: en dessinant trois ensembles qui se coupent (A,B et X). Il y a 7 zones. On les étudie une par une.
Si z est dans A mais pas dans B ni dans X. Alors z est dans
Tu pourras de même éliminer les 2 autres zones où on appartient à un seul des trois ensembles, et également celle où on appartient aux trois simultanément.
Bilan. On est toujours dans exactement deux ensembles:
si on est dans A et B, on n'est pas dans X.
Si on est dans X, on est soit dans A, soit dans B.
D'où
Synthèse immédiate. :happy2:
sue a écrit:n'a-t-on pas une CS B inclus dans A ? ce qui restreint la solution à A\B .
Ce serait une CN, non?
Et d'autre part, je ne vois pas pourquoi.
Si on prend z dans
soit z est dans A et pas dans X. Pas dans X, cela siginife dans ni dans A ni dans B (absurde) ou dans les deux. Conclusion z est dans B.
soit z est dans X est pas dans A. Dans ce cas, z est dans B.
Donc
Réciproquement, si z est dans B,
soit il est dans A, et donc, il ne sera pas dans
soit il n'est pas dans A. Auquel cas, il est dans
Donc B est bien inclus dans
Oui Ok , ça va , je crois que j'ai compris !
en fait , je suis allée un peu vite , j'ai dit ben on a : , donc B est inclus dans AUX et pas dans l'inter , par miracle on conclut que B est inclus dans A et n'intersecte pas avec X !!! :hum:
, donc B est inclus dans AUX et pas dans l'inter , par miracle on conclut que B est inclus dans A et n'intersecte pas avec X !!! :hum:
comme punition ..euh comme exercice :ptdr: j'essaierai de vérifier que c'est bien égale à B !
en fait , je suis allée un peu vite , j'ai dit ben on a :
comme punition ..euh comme exercice :ptdr: j'essaierai de vérifier que c'est bien égale à B !
enfin , je tombe bien sur B :we: (aprés avoir refait le dévellopement :hum:).
mais j'avoues que ça m'a inquièté un tit peu le fait qu'il ait UNE solution , généralement ce n'est pas le cas . c'est la 1ère (sur un total de 4 faite :ptdr: ) qui admet une seule soluce .
merci Emdro !
sinon t'as pas une autre équation à me proposer ?
mais j'avoues que ça m'a inquièté un tit peu le fait qu'il ait UNE solution , généralement ce n'est pas le cas . c'est la 1ère (sur un total de 4 faite :ptdr: ) qui admet une seule soluce .
merci Emdro !
sinon t'as pas une autre équation à me proposer ?
Tu es courageuse!
De viens de retrouver mon premier cahier d'exos de sup!
1.facile: Soient A, B, C trois parties d'une ensemble E. Montrer que si et
et 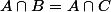 alors B=C.
alors B=C.
2.Soit E un ensemble, A une partie de E. Le but est de trouver tous les couples (X,Y) de parties de E telles que .
.
a. Soient R et S deux parties arbitraires de E. Montrer que) et
et ) sont solutions du problème.
sont solutions du problème.
b. Monter que réciproquement toute solution (X,Y) du problème est nécessairement de la forme ci-dessus.
De viens de retrouver mon premier cahier d'exos de sup!
1.facile: Soient A, B, C trois parties d'une ensemble E. Montrer que si
2.Soit E un ensemble, A une partie de E. Le but est de trouver tous les couples (X,Y) de parties de E telles que
a. Soient R et S deux parties arbitraires de E. Montrer que
b. Monter que réciproquement toute solution (X,Y) du problème est nécessairement de la forme ci-dessus.
pour le 1er, on suppose que  et
et 
soit x dans B alors il est dans AUB soit dans AUC , donc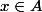 ou
ou 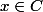
-si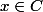 alors B est inclus dans C
alors B est inclus dans C
- si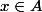 alors
alors 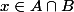 , soit
, soit 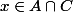 et donc
et donc 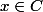
finalement , on a dns tous les cas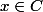 i.e B est inclus dans C
i.e B est inclus dans C
par symétrie de rôle , on prouve que C est aussi inclus dans B , soit B=C .
mais je doute que ça soit la solution (si c juste bien sur) la plus directe .
pour le 2ème , la a est simple suffit de vérifier , je tombe à la fin sur qui est égale à A donc c bon .
qui est égale à A donc c bon .
sinon je cherche toujours la réciproque .
soit x dans B alors il est dans AUB soit dans AUC , donc
-si
- si
finalement , on a dns tous les cas
par symétrie de rôle , on prouve que C est aussi inclus dans B , soit B=C .
mais je doute que ça soit la solution (si c juste bien sur) la plus directe .
pour le 2ème , la a est simple suffit de vérifier , je tombe à la fin sur
sinon je cherche toujours la réciproque .
65 messages
- Page 2 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
