Revisions spé supplémentarité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 16 Sep 2010, 19:24
par benekire2 » 16 Sep 2010, 19:24
girdav a écrit:Salut benekire2,
tu peux évaluer l'égalité pour les matrices élémentaires

, c'est-à-dire les matrices dont tous les termes sont nuls sauf le terme de la ligne

et colonne

qui vaut

.
Salut girdav !
Merci pour la méthode, :we:
-
Matheur69
- Membre Naturel
- Messages: 12
- Enregistré le: 15 Sep 2010, 16:59
-
 par Matheur69 » 16 Sep 2010, 21:09
par Matheur69 » 16 Sep 2010, 21:09
Encore un little problem :
Il faut montrer que pour toute matrice M de M_n(C) il existe un complexe k tel que M-kId ne soit pas inversible.
Je dit que il existe un polynôme P non nul tel que P(M)=0 et que donc avec les a_i racines de P , (M-a_1)...(M-a_n)=0
Mais je ne vois pas comment conclure. Merci de votre aide !
PS : Par ailleurs il faut en déduire ensuite que il existe une matrice X telle que MX=kX et donc en gros faudrait prouver qu'on peut trouver une matrice X telle que (M-kId)X=0 et vois pas non plus ,
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Sep 2010, 21:14
par Nightmare » 16 Sep 2010, 21:14
Que signifie M-a1 ? D'où vient ce polynôme P ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 16 Sep 2010, 22:05
par girdav » 16 Sep 2010, 22:05
Matheur69 a écrit:Encore un little problem :
Il faut montrer que pour toute matrice M de M_n(C) il existe un complexe k tel que M-kId ne soit pas inversible.
Pense en terme de déterminants.
-
Matheur69
- Membre Naturel
- Messages: 12
- Enregistré le: 15 Sep 2010, 16:59
-
 par Matheur69 » 17 Sep 2010, 06:46
par Matheur69 » 17 Sep 2010, 06:46
P est un polynome qui annule M et les a_i sont les racines de ce polynôme. Peut on s'en sortir sans déterminant ?
-
Matheur69
- Membre Naturel
- Messages: 12
- Enregistré le: 15 Sep 2010, 16:59
-
 par Matheur69 » 17 Sep 2010, 08:59
par Matheur69 » 17 Sep 2010, 08:59
Mais ca me dit toujours pas comment montrer que M-k*Id n'est pas inversible pour un certain k,
par contre ca solutione ma deuxième question
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Sep 2010, 10:10
par girdav » 17 Sep 2010, 10:10
Comment établis-tu l'existence de ce polynôme? De plus, je crois qu'il faut écrire les facteurs

avec

la matrice identité, car les

sont des complexes. Arrivé là, tu peux déduire qu'il y a au moins une matrice de la forme

qui n'est pas inversible, sinon le produit le serait.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Sep 2010, 10:38
par Nightmare » 17 Sep 2010, 10:38
Matheur69 a écrit:P est un polynome qui annule M et les a_i sont les racines de ce polynôme. Peut on s'en sortir sans déterminant ?
Cela ne répond pas à ma question, qu'est-ce qui assure l'existence de P? Et surtout, pourquoi introduire ce polynôme P si tu ne sais pas quoi en faire? Je veux dire, c'est pas anodin que de parler d'un tel polynôme...
Sinon, la méthode proposée par Girdav est essentiellement la même.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Sep 2010, 11:00
par girdav » 17 Sep 2010, 11:00
Oui, il serait dommage d'établir l'existence d'un polynôme annulateur avec des outils plus sophistiqués que le déterminant.
-
Matheur69
- Membre Naturel
- Messages: 12
- Enregistré le: 15 Sep 2010, 16:59
-
 par Matheur69 » 17 Sep 2010, 12:15
par Matheur69 » 17 Sep 2010, 12:15
D'accord merci
En effet on demandait avant dans l'exercice de montrer que il existait un tel polynôme or (Id,M...M^n) est forcement libre a un moment,
Sinon un autre problème je dois expliciter les suites u et v telles que:
u0=0 et v1=1 vérifiant

et
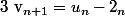
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
, c'est-à-dire les matrices dont tous les termes sont nuls sauf le terme de la ligne
et colonne
qui vaut
.