Révisions...

[emdro]

oui, c'est ça! :++:

[sue]

Ok :we:
je prend mon repas et je regarde l'autre exo !

[emdro]

Itadakimass! :fr: :beer:

[sue]

merci ! :happy2:

ben je commence par le plus simple :
= (A\ B)inter (B\ A) = (B\ A)inter (A\ B) = !
pour la distributivité de par rapport à , je vois pas mon erreur ici :

or, !
sinon pour l'associativité , je vois déjà un dévellopement trop long , j'vais voir si on peut faire plus simple !

[emdro]

Pour l'associativité, ce n'est pas difficile, mais super long. Je pense que tu ne pourras pas y couper!

Pour la distributivité, pas d'erreur. Reste à monter que tes expressions donnent en fait la même chose (fais un dessin...)

[sue]

mais ouf enfin :fan:



sinon pour la distributivité Ok !

[sue]

bonne nuit et merci pour ces exos sympas :we:

[emdro]

Encore un exo si tu veux (pas difficile):

Soit E un ensemble et A,B des parties de E. On définit l'application f de P(E) dans P(A)xP(B) par . [P(T) est l'ensemble des parties de T]
A quelle condition doivent satisfaire A et B pour que f soit injective? pour que f soit surjective?

[sue]

ohayou!

Oui bien sûr , merci .
dsl si je répond tard , c que je ne peux pas avoir accés à internet chaque jour .

sinon pour l'exo je crois que la condition pour l'injectivité est , je cherche encore pour la surjectivité .
soient

soient et

et puisque f est injective alors .

[emdro]

Ohayou!

C'est bon!

[sue]

ben voilà , si f est surjective alors tq soit, et i.e , c'est la condition .

[emdro]

C'est nécéssaire, mais pas suffisant...

[sue]

faut donc vérifier la réciproque ..
soient et
on a

[emdro]

C'est bon!

NB J'ai un peu honte: j'avais gardé en tête la condition et je n'ai pas vu que B inclus dans le complémentaire de A revenait au même! Disons que c'est parce qu'il est un peu tôt... :briques:

[sue]

no problemo!

ben disons moi c pire , en revenant un peu en arrière , je ne comprend même pas ce que j'avais écris l'autre soir :doh:

mais ouf enfin :fan:

euh, me semble que c faux !!
tt ce que j'ai sur mon papier :

et
c clair que :
mais sinon et ne veulent pas dire la même chose !
je crois que j'avais considéré les ensembles disjoints ou un truc du genre :briques:

[sue]

en faisant appel à la fonction caractéristique je tombe bien sur le résultat , mais bon je vois pas mon erreur là !!

[emdro]

J'ai retrouvé mon cahier de sup: l'expression charnière pour et était:


(en 7 étapes!)

[sue]

ben j'ai un peu la flemme de retrouver cette expression :triste:
mais bon avec la fct caractéristique on trouve :
et par symétrie de A B et C on conclut .
en vérifiant ça colle bien avec ton expression ! :we:

sinon , je me demande quand est-ce qu'on peut pas utiliser la fct phi pour ce genre d'exo !
on a vu cette fonction juste dans un exo , si mes souvenirs sont bons , donc je l'ai pas dans mon cours !

[emdro]

Je n'avais pas pensé à la fonction caractéristique. Je ne vois pas comme ça de cas où elle n'est pas utilisable (puisque tu sais exprimer à l'aide de phi, les opérations de base: union, intersection, complémentaire). A condition quand même de préciser de quoi tu parles: Soit Phi la fonction caractéristique...

As-tu essayé de résoudre l'équation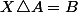 qui te posait problème, avec cet outil?

Sinon, je crois que c'est bon pour le premier chapitre de sup! Tu es au point! Passe à la suite... :++:

[sue]

je n'y avais pas pensé pour l'équation !
en fait je ne vois pas comment faire , ça sert juste pour vérifier une fois on a la solution , mais je vais regardé de plus prés cet aprèm , car là je dois quitter .

sinon Oui , je crois que je vais passer aux structures algébriques , juste une brève révision , parce que c'était la dernière chose qu'on a vu et en parallèle un peu des applications .

merci pour tout c'est trés sympa :we:
have a great time !