Résoudre ln d'un complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathelot
 par mathelot » 10 Juin 2021, 11:33
par mathelot » 10 Juin 2021, 11:33
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 10 Juin 2021, 12:02
par Pisigma » 10 Juin 2021, 12:02
Bonjour,
c'est la forme exponentielle de
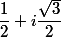
-
Black Jack
 par Black Jack » 10 Juin 2021, 12:04
par Black Jack » 10 Juin 2021, 12:04
cos(Pi/3) + i.sin(Pi/3) = e^(i.Pi/3)
et avec cos(Pi/3) = 1/2 et sin(Pi/3) = (V3)/2 --> 1/2 + i.(V3)/2 = e^(i.Pi/3)
Mais on a aussi : 1/2 + i.(V3)/2 = e^(i.(Pi/3 + 2k.Pi))

-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 10 Juin 2021, 12:19
par GaBuZoMeu » 10 Juin 2021, 12:19
Bonjour.
Facile ! Le module de

est 1, le logarithme du module est 0.
La détermination principale de l'argument de

est
)
.
Donc
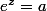
si et seulement si

est de la forme
+2k\pi))
avec
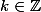
.
Modifié en dernier par
GaBuZoMeu le 10 Juin 2021, 13:22, modifié 2 fois.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 10 Juin 2021, 12:46
par GaBuZoMeu » 10 Juin 2021, 12:46
Merci pour cette franche rigolade : "C'est pas manuel" !
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 10 Juin 2021, 13:01
par GaBuZoMeu » 10 Juin 2021, 13:01
Tu calcules le logarithme d'un nombre réel >0 de tête, toi ?
Et je tape manuellement sur mon clavier pour calculer l'arccos d'un nombre dans [-1,1].
Je peux aussi ressortir ma vieille règle à calcul (entièrement manuelle).
Franchement, je ne comprends pas ce que tu cherches.
-
mathelot
 par mathelot » 10 Juin 2021, 15:14
par mathelot » 10 Juin 2021, 15:14
lazare a écrit: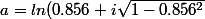)
on pose
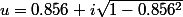
et

un argument de u.
on a |u|=1 (le module de u vaut 1)
et
=\dfrac{sin(\theta)}{cos(\theta)}=\dfrac{\sqrt{1 - 0.856^2}}{0.856 }=0.6039437167)
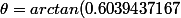=0.5433142474)
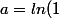+i 0.5433142474=i \, (0.5433142474))
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 10 Juin 2021, 15:45
par GaBuZoMeu » 10 Juin 2021, 15:45
Mais voyons, mathelot, tu n'as pas calculé arctan( ) manuellement ! Et je soupçonne même que tu as fait appel à une machine pour calculer
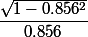
!
-
mathelot
 par mathelot » 10 Juin 2021, 16:02
par mathelot » 10 Juin 2021, 16:02
GaBuZoMeu a écrit:Mais voyons, mathelot, tu n'as pas calculé arctan( ) manuellement ! Et je soupçonne même que tu as fait appel à une machine pour calculer
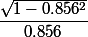
!
oui, mea maxime culpa

-
Black Jack
 par Black Jack » 10 Juin 2021, 18:46
par Black Jack » 10 Juin 2021, 18:46
lazare a écrit: GaBuZoMeu a écrit:Tu calcules le logarithme d'un nombre réel >0 de tête, toi ?
Et je tape manuellement sur mon clavier pour calculer l'arccos d'un nombre dans [-1,1].
Je peux aussi ressortir ma vieille règle à calcul (entièrement manuelle).
Franchement, je ne comprends pas ce que tu cherches.
Haha, je sais pas, comment les machines sont programées pour le calculer?
Comment les gens faisaient avant les machines ?
Avec des "tables" , dont voici une toute petite partie :
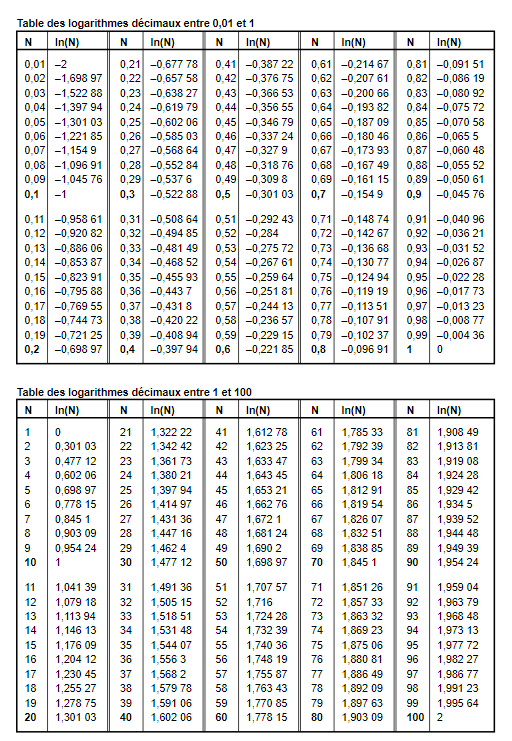
-
azf
 par azf » 10 Juin 2021, 19:14
par azf » 10 Juin 2021, 19:14
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
!

