Salut,
A mon avis (ça vaut ce que ça vaut...) plutôt que de regarder les cas particulier, il me semble plus "sain" de commencer par le cas le plus fréquent : l'intersection de deux sphères, c'est (sauf exceptions) un cercle [ou l'ensemble vide] puis l'intersection d'un cercle et d'une sphère, c'est (sauf exceptions) deux points [ou vide].
Donc ton système, (sauf exceptions), il a zéro ou deux solutions. Et ça, ça signifie quasi surement que (sauf exceptions) tout va se ramener à une équation du second degré à résoudre.
Et effectivement, si tu regarde les équations L2-L1 et L3-L1 (*) ça te donne un système
linéaire de 2 équations à 3 inconnues (x,y,z) qui, si on le résous, permet (sauf exceptions) d'exprimer par exemple x et y linéairement en fonction de z. Et y'a plus qu'à réinjecter ça dans la L1 pour obtenir une équation du second degré en z qui va "piloter" le nombre de solutions.
Sinon, ça :
pascal16 a écrit:si on appelle L1, L 2 et L3 les 3 lignes de ton système, remplace le par
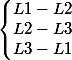
C'est évidement le truc qu'il
ne faut pas écrire : déjà, la 3em ligne du nouveau systèmevu que c'est l'opposé de la somme des deux premières, elle ne sert évidement à rien. Et ensuite, (comme par hasard) partant de ces 3 équation là, tu ne peut retrouver (par combinaison linéaire) ni L1, ni L2, ni L3 donc ce système là n'implique aucune des équation du système de départ.
Bref, avec un système, au fond, tu peut faire "un peu tout et n'importe quoi", mais il faut évidement t'assurer que ce que tu écrit est
équivalent au problème de départ (i.e. que les nouvelles équations
impliquent les anciennes)

