Récurrence multiple (et autres questions sur les suites)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 12 Déc 2012, 01:35
par Skullkid » 12 Déc 2012, 01:35
Kikoo <3 Bieber a écrit:Première partie, c'est immédiat vu que la suite diverge vers - l'infini (on utilise alors la définition d'une telle suite et on fixe un réel qui vaut -2).
Bonsoir, est-ce si immédiat ? Si a est dans [0,1] ta suite va converger. Pour la propriété à démontrer par récurrence, si on prend a = -1, alors u1 = -2 et u2 = -6 n'est pas inférieur à -2^(2^2) = -16. Le truc à démontrer ce serait pas plutôt
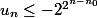
?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 12 Déc 2012, 17:55
par Kikoo <3 Bieber » 12 Déc 2012, 17:55
Skullkid a écrit:Bonsoir, est-ce si immédiat ? Si a est dans [0,1] ta suite va converger. Pour la propriété à démontrer par récurrence, si on prend a = -1, alors u1 = -2 et u2 = -6 n'est pas inférieur à -2^(2^2) = -16. Le truc à démontrer ce serait pas plutôt
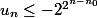
?
Salut Skullkid !
J'avais oublié de préciser qu'effectivement, je travaille pour tout a inférieur strictement à 0, et cela revient au même que d'étudier la suite lorsque le premier terme dépasse strictement 1.
Justement, j'avais essayé de faire une récurrence, mais mon initialisation bloquait (l'hérédité non !)... Et il s'agit de la formule que j'ai.
Je verrai sur la correction qu'il nous apportera demain, car il n'est pas spécifié que l'on doive démontrer ceci par récurrence. Il se peut que je me sois trompé dans mon raisonnement.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 13 Déc 2012, 21:59
par Kikoo <3 Bieber » 13 Déc 2012, 21:59
Erratum : en effet, il s'agit plutôt n-n0 :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
