Se ramener à un recouvrement dénombrable pour un espace métr

[pangloss]

Bonjour! Tu es nouveau ici. Je te prie d'aller lire le réglement du forum et de le respecter!

Je n'arrive pas à résoudre le problème suivant:


Comment montrer qu'un espace métrique (E, d) est compact pourvu qu'il vérifie la propriété suivante (qui semble à première vue plus faible que la propriété de Borel-Lebesgue): de tout sous-recouvrement dénombrable d'ouverts de E on peut extraire un sous-recouvrement fini.

Merci pour l'aide.

[Zavonen]

Cela me parait vrai pour un espace séparable (possédant un sous-ensemble dense dénombrable). Mais en toute généralité ???

[amstramgram]

Salut !

Pour tout espace métrique X, on a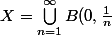 . C'est un recouvrement dénombrable de X par des ouverts. Comme tous les ouverts s'écrivent comme des réunions dénombrables de boules, on doit pouvoir se ramener à un recouvrement comme celui-ci à partir de n'importe quel recouvrement par des ouverts.

C'est pas vraiment une preuve en fait, mais si ça peut donner une idée... :we:

[Nightmare]

Salut !

Il nous faut un argument de séparabilité sinon c'est faux ! Ceci étant dit, il reste à montrer que de tout recouvrement par des ouverts on peut extraire un sous-recouvrement dénombrable et par hypothèse on pourra donc extraire un sous-recouvrement fini ! Je te laisse essayer de faire cela ! (pense a utiliser une base dénombrable de X)

[arttle]

Heu je pense que je vais dire une bêtise, mais quand je lis l'exercice je vois ça en hypothèses :
(E,d) espace métrique qui possède la propriété que de tout recouvrement dénombrable de E par des ouverts on peut extraire un recouvrement fini
et en conclusion :
E est compact

j'ai l'impression que tout le monde démontre que de tout recouvrement dénombrable on peut extraire un recouvrement fini dans un espace métrique compact

[Nightmare]

arttle > Non ce n'est pas ce que j'ai proposé de prouvé !

[pangloss]

Merci pour ces nombreuses réponses. J'y réponds dans l'ordre.

D'abord, l'énoncé ne stipule absolument aucune hypothèse de séparabilité.

Ensuite, même si on acceptre cette hypothèse, je ne trouve pas évident qu'elle nous aide véritablement. Même si l'espace est séparable, disons s'il admet le sous ensemble dense: a0..an... Il ne me semble pas que cela nous permette directement d'extraire un sous-recouvrement dénombrable de tout recouvrement. Il me semble qu'il est faux de penser qu'en partant d'un recouvrement quelconque, il suffirait de conserver un seul des ouverts du recouvrement pour chaque ai.

Nightmare, peux-tu me donner un exemple d'espace métrique non-séparable vérifiant la pseudo-propriété de Lebesgue (avec dénombrabilité du recouvrement) mais non pas la véritable propriété de Lebesgue?