Bon, j'ai un peu la haine là, je venais de taper une réponse, et j'étais pas loggué, donc mon message a été effacé ... Enfin passons, je vais le retaper.
Donc j'ai commencé les calculs hier soir, je t'explique ma démarche (le but ultime étant pour moi de trouver

).
Déjà, j'ai eu exactement la même idée que toi concernant l'emplacement du cercle

, j'ai pris son centre en
)
.
J'ai ensuite pris un repère orthonormé
)
.
Voilà alors ma démarche :
Les seules variables sont R et R'.
On veut au final calculer l'aire des intersections, donc on devrait aboutir à un calcul d'intégrale double : il faut les bornes.
1) On cherche les équations des trois cercles
On a déjà facilement
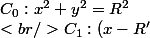^2 + y^2 = R^2)
2) Pour

, il faut trouver les points d'intersection entre
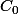
et

, puis on en choisit un arbitrairement, et on prend

de rayon

, qui passe par ce point, et dont le centre est à une distance
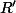
de

.
J'arrive aux coordonnées du centre de

:
R'^4}{4R^4},\frac{\sqrt{4R^2-R'^2}R'^2}{2R^2}\right))
Au passage, la condition

est apparue, pour l'existence d'un point d'intersection (elle était d'ailleurs relativement évidente). Il doit donc y avoir une zone sur ton graphe où

n'est pas définie. Ce qui semble être le cas (d'ailleurs, si tu pouvais nommer tes axes, ça serait sympa).
Ensuite, il ne reste "qu'à" calculer les trois intégrales, ce que je n'ai pas encore fait, car cela semble technique. Dis moi déjà si tu as les même résultats que moi pour l'instant.
