Racines primitives de l'unité

[Kurt Gödel]

Bonjour,

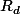
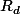
Si je note l'ensemble des racines primitives d-iemes de l'unité, pourquoi est-ce que l'ensemble des , lorsque décrit l'ensemble des diviseurs positifs de , forme une partition de ensemble des rainces n-iemes de l'unité?

Merci.

[benekire2]

Salut, d'abord tu as sans doute remarqué que tes R_d sont disjoints (reviens à la definition des racines de l'unité) . Enfin, il est simple de montrer que toute racine de l'unité est une racine primitive d'un diviseur de n. En effet z racine => z=e^((i*k*pi)/n)=e^((i*'k*q*pi)/(n'*q)) avec q le pgcd de k et n . Ainsi ta racine devient primitive puisque pgcd(n',k')=1

Avec ça on en déduit plein de choses ... et actuellement je me casse les dents sur ces foutus polynômes cyclotomiques.

[Kurt Gödel]

J'ai toujours pas compris pourquoi votre démonstration prouve la partition? Pouvez-vous expliquer plus clairement? Merci.

[Nightmare]

Salut,

Une racine primitive n-ème de l'unité c'est un générateur du groupe cyclique d'ordre n des racines n-ème de l'unité. A partir de là, il est clair que lorsqu'on est une racine primitive n-ème de l'unité, on ne peut être une racine primitive m-ème pour m différent de n. En outre, chaque racine p-ème de l'unité engendre un groupe d'ordre d () formé des racines d-ème de l'unité. C'est donc une racine primitive d-ème de l'unité. Autrement dit, toute racine de l'unité est racine primitive son-ordre-ème de l'unité.

[benekire2]

J'ai montré que la réunion des R_d faisait l'ensemble des racines n-ième de l'unité. Pour prouver la partition il faut et il suffit de montrer la disjonction. C'est pas super dur :


qui se réécrit encore kd'=k'd et donc par le théorème de Gauss, k divise k' et d' divise d et donc il existe p et p' tel que kd'=kpd'p' ie pp'=1 ie p=1 et p'=1 et donc tes deux racines primitives sont forcément égales.

Sauf erreur.