Question vrai/faux

[Yokidok]

Bonjour,
Je suis bloqué à une question dont voici l'énoncé :

La fonction définie par la formule
f(x) = ln((exp(x) - 1)/x)
Admet un prolongement de classe C1 au voisinage de 0.
Ce prolongement est localement au dessus de sa tangente en 0.

Je ne comprend pas...
Jessai de faire un DL en 0 à l'ordre 2 ou 3 vu que l'énoncé est au voisinage de 0 mais je parviens pas à répondre.

[phyelec]

bonjour,

le DL de exp(x) au voisinage de 0 est 1+x

donc au voisinage de 0 : exp(x) -1 =1+x-1=x

donc au voisinage de 0 ln((exp(x) - 1)/x)= ln(x/x)=ln(1)=0

[Yokidok]

Okay donc la on prouve que f est prolongeable par continuité en 0

[phyelec]

sur quel intervalle est votre fonction?

[Yokidok]

Elle est définie sur R privé de 0 non ?

[phyelec]

la fonction logarithme népérien est définie sur ]0,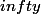

donc (exp(x)-1)/x doit toujours être positif et supérieur à 0

[phyelec]

lire +l'infini

[Yokidok]

Quand je la trace sur la calculatrice ce n'est pas le cas

[Black Jack]

Bonjour,

f(x) = ln((exp(x) - 1)/x)

g(x) = (exp(x) - 1)/x

lim(x-->0) g(x) est une indétermination du type 0/0 --> Lhospital
lim(x-->0) g(x) = lim(x-->0) exp(x)/1 = 1

Et donc lim(x-->0) f(x) = ln(1) = 0

f(x) peut être prolongé en 0 par :

f(x) = ln((exp(x) - 1)/x) pour x dans R/{0}
f(0) = 0

Reste à vérifier si ainsi défini f est dérivable en 0.

lim( x--> 0) [(f(x) - f(0))/x] = lim( x--> 0) [(ln((exp(x) - 1)/x))/x] --> (Lhospital) = lim( x--> 0) [(x/(exp(x) - 1)) * ((x.exp(x) + 1 - exp(x))/(x²))]
= lim( x--> 0) [(((x.exp(x) + 1 - exp(x))/(x.(exp(x) - 1)))] --> (Lhospital) = lim( x--> 0) [(((exp(x) + x.exp(x) - exp(x))/((exp(x) - 1) + x.exp(x)))]
= lim( x--> 0) [(x.exp(x))/((exp(x) - 1) + x.exp(x)))] --> (Lhospital) = lim( x--> 0) [(exp(x) + x.exp(x))/(exp(x) + x.exp(x) + exp(x)] = 1/2

--> f est dérivable en 0 et f'(0) = 1/2
et donc f (prolongé par f(0) = 0) est dérivable sur R.

Et si on ne connait pas la règle de Lhospital .... reste à trouver une autre méthode.

[Yokidok]

Merci et comment savoir si elle ce prolongement est au dessus de sa tangente

[Black Jack]

Bonjour,

Je ne sais pas trop ce qui est demandé ... (mais je ne suis pas matheux)

La tangente à Cf au point d'abscisse a a pour équation : Ta : y = (x - a) * (e^a . (a-1) + 1)/(a.(e^a - 1)) + ln((e^a - 1)/a)

Et si a --> 0 : y = x/2 (approximation de l'équation de la tangente près de 0)

Quoi faire avec cela ? Je n'en sais rien.

Attendre la réponse d'un matheux.