Salut,
Le problème (récurrent ces derniers temps), c'est que tu te pose la question complètement "à l'envers" de ce qui serait logique : Tu te demande "a-t-on le
le droit de faire ça" alors qu'à mon sens, la question à se poser c'est (évidement) "Quelle est la
définition du ça en question" et que c'est évidement de ce coté là qu'il faut chercher la/les réponse pour savoir si "on a le droit" ou pas de le faire.
Pour reprendre ton exemple archi simple de division par 0, il me semble quand même que c'est
nettement plus malin, plutôt que de simplement dire "on a
pas le droit de diviser par zéro", c'est de se rappeler que la définition même d'une division, c'est "l'inverse d'une multiplication", c'est à dire que 3/5, c'est le nombre qui, multiplié par 5 donne 3. Et concernant la fameuse division par 0, ben 3/0, normalement ça devrait être le nombre qui, multiplié par 0 donne 3 sauf que... y'en a pas... Et c'est pas con du tout de comprendre ça aussi (surtout) du fait que concernant 0/0, c'est pas la même problème : des nombre qui, multiplié par 0 donnent 0, c'est pas qu'il n'y en a pas, c'est que n'importe quel nombre multiplié par 0 donne 0, donc que 0/0, ben ça désigne pas un nombre en particulier, mais plutôt ça désigne
tout les nombres (alors que 3/0, ben ça désigne personne).
Bon, sinon, pour en revenir au puissances,
les (y'en a plusieurs) définition qu'on voit à l'école, c'est (dans cet ordre) :
(1) Si n est un entier naturel au moins égal à 1 et A un réel quelconque (voire un complexe, ou une matrice ou des tas d'autre chose) A^n, c'est AxAx...xA où le A apparait n fois.
(2) On constate qu'en fait, pour "passer" de A^n à A^(n+1), ben faut multiplier par A, donc dans l'autre sens,
si A est non nul, ça veut dire que pour passer de A^n à A^(n-1), ben il faut diviser par A et ça conduit naturellement à poser A^0=A^1/A=A/A=1, puis A^(-1)=A^0/A=1/A A^(-2)=A^(-1)/A=1/A², etc
Mais toutes ces nouvelles définitions ne sont valables que pour A non nul : on accepte "plus" de valeurs pour l'exposant (des négatifs ou nuls) mais moins de valeurs pour le terme dont on prend la puissance (il doit être non nul)
(3) On vérifie alors que, pour tout n et m entiers et tout réel A (non nul si certains des exposant son négatifs) on a (A^n)(A^m)=A^(n+m) et que (A^n)^m=A^(nm) et ça donne une nouvelle idée pour "généraliser" la notion d'exposants, par exemple, si on veut définir A^(1/2), ben ça serait logique que (A^1/2))^2=A^1=A donc que A^(1/2) soit un réel qui au carré donne A. Sauf que c'est la merde vu que, si A>0, ben des réels qui au carré donne A, y'en a deux et que, si A<0, ben y'en a pas. Si A est <0, y'a pas moyen de s'en sortir (pas de solution), mais s'il est >0, on peut s'en sortir en choisissant
arbitrairement que A^(1/2) c'est le nombre
positif dont le carré donne A, c'est à dire la racine de A (idem pour tout les A^(1/n) avec n pair où on prend arbitrairement
la solution positive).
Et là où on voit que c'est super chiant ce "choix arbitraire", c'est que maintenant, avec cette nouvelle définition, ben y'a des cas où (A^b)^c existe, mais où il n'est pas égal à A^(bc), par exemple (A^2)^(1/2), ça existe y compris quand A est négatif, mais par contre dans ce cas là, c'est pas égal à A^1=A, mais à -A.
Pour l'exposant 1/3 (et de façon générale pour les 1/n avec n impair), c'est la même chose, on aimerais bien définir A^(1/3) comme étant un réel qui, au cube donne A et là, c'est du pot, que A soit négatif ou positif, ben y'a toujours un unique réel qui au cube donne A donc on peut dire éventuellement dire que c'est lui qui vaut A^(1/3) donc que c'est la racine cubique de A.
Ensuite, ben on peut si on veut tenter de continuer à généraliser la définition en disant par exemple que A^(4/3), c'est le nombre qui au cube donne A^4 et ce nombre va exister que A soit positif ou négatif vu que tout réel positif ou négatif est le cube d'un autre réel.
Sauf que la plupart des matheux (dont moi) ainsi que la grande majorité des "outils informatique" refusent cette définition là vu qu'elle a un coté complètement aberrant : les nombres 5/3 et 10/6 sont totalement parfaitement égaux, mais, si A<0, alors A^(5/3) (= l'unique réel qui au cube donne A^5, et qui est négatif) n'est pas égal à A^(8/6) (= le réel positif qui à la puissance 6 donne A^8) ce qui parait profondément débile.
Et tout ton questionnement, en fait, il revient à cette question : faut-il accepter ou pas d'élever des nombres négatifs à des puissance fractionnaires avec l'énorme risque d'écrire des trucs complètement faux rapidement ?
Et par exemple, je t'inciterais fortement à tenter ce type d'écriture sur différentes calculettes, différents tableurs, différents logiciels de calcul formel ou de calcul numérique pour voir que certain (assez rare) trucs acceptent cette écriture, mais que la majorité la refusent.
(et si tu veut mon avis, en math, il est infiniment plus "sain" de la refuser et d'écrire
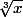
et pas
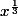
lorsque l'on veut accepter les x négatifs)
P.S. Et si ça t'intéresse, avec A non nul (et éventuellement négatif) et B absolument quelconque, il y a plus ou moins moyen de "définir" ce qu'est A^B, sauf que ça ne désigne plus
UN nombre réel, mais en fait
PLUSIEURS nombre complexes (exactement de la même façon qu'il est souvent bien plus malin de parler DES racines carrées de 4 qui sont 2 et -2 plutôt que de parler de LA racine carré de 4 : c.f. le coté arbitraire d'avoir chois la solution positive comme étant LA racine carré)
Par exemple, on parle très très souvent DES racines cinquième du réel -1 (qui a 5 racines cinquièmes).
Et on pourrait éventuellement parler de (-1)^Pi qui, au fond, désigne un ensemble
infini de nombres complexes.
