Puissance des nombres complexes et angle droit

[musique137]

Bonjour,

J'ai un exercice sur les complexes où je bloque un peu.

Soit M1, M2 et M3 d'affixes respectives z, z², z^3. z désigne un nombre complexe.

1) Déterminer l'ensemble des nombres complexes z tels que les points M1, M2 et M3
soient deux à deux distincts.

2) On suppose les points M1, M2 et M3 deux à deux distincts. Déterminer l'ensemble
des points M1 tels que l'un des angles du triangle M1, M2 et M3 soit un angle droit.

Si quelqu'un a une idée merci !

[musique137]

Pour z ≠ z² j'ai commencé par faire :

z = a + ib et z² = (a + ib)² = a² + 2aib - b².

Donc on veut :

a ≠ a² - b²
et
b ≠ 2ab soit a ≠ 1/2

[Carpate]

et distincts pour tout point M du plan complexe dont l'affixe z n'est pas solution de soit donc pour tout point du plan à l'exception des points d'affixe ... et ...

[musique137]

Merci de la réponse rapide, très bien je vois comment faire maintenant merci

[musique137]

Par contre pour l'angle je bloque toujours

[Carpate]

Prenons le cas rectangle en :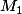
Les vecteurs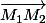 et sont orthogonaux
Traduis cela en une relation entre leurs affixes

[musique137]

Si les vecteurs M1M2 et M1M3 sont orthogonaux alors leur affixe Z( trouver avec Z=(z²-z)/(z^3-z) ) est un nombre imaginaire pure.

Z = ( z-1)/(z²-1) = (a + ib - 1) / (a² + 2aib - b² - 1).

On veut : a - 1 = 0 donc a = 1
et
a² - b² - 1 = 0 donc b = O.

J'obtiens z = 1. (ce complexe est exclu car sinon M1, M2 et M3 ne sont plus distincts deux à deux)

[Carpate]

[zygomatique]

salut

1/ c'est insuffisant

il faut ces deux inégalités impliquant que

or

2/ un triangle possède trois angles ...

[musique137]

Pour qu'un nombre réel soit égal à un nombre imaginaire il faut que les
deux soient nuls.

Donc z² - z = 0 et z^3 - z =0.

z² = z^3
z = 1

[musique137]

salut

1/ c'est insuffisant

il faut ces deux inégalités impliquant que

or

2/ un triangle possède trois angles ...

Merci de ta réponse, oui pour le 1 c'est insuffisant mais Carpate me donnait juste une piste pour commencer. Après j'ai trouvé - 1, 0 et 1.

Et pour le 2 c'est pareil, Carpate me donne une piste pour commencer.

[Pseuda]

Pour qu'un nombre réel soit égal à un nombre imaginaire il faut que les
deux soient nuls.

Donc z² - z = 0 et z^3 - z =0.

z² = z^3
z = 1

Bonsoir,

Où vois-tu un nombre réel et un nombre imaginaire dans z²-z et z^3-z ?

Il faut simplement résoudre l'équation obtenue (en fait il y a en deux en une) d'inconnue z. Et il reste d'autres équations à résoudre.

[chan79]

Il y a une infinité de solutions

[Pseuda]

Si les vecteurs M1M2 et M1M3 sont orthogonaux alors leur affixe Z( trouver avec Z=(z²-z)/(z^3-z) ) est un nombre imaginaire pure.

Z = ( z-1)/(z²-1) = (a + ib - 1) / (a² + 2aib - b² - 1).

On veut : a - 1 = 0 donc a = 1
et
a² - b² - 1 = 0 donc b = O.

J'obtiens z = 1. (ce complexe est exclu car sinon M1, M2 et M3 ne sont plus distincts deux à deux)

Bonjour,

En gras : oui, mais la démarche ensuite n'est pas la plus simple : reste le plus possible avec le complexe z, c'est-à-dire qu'il est inutile et plus compliqué de revenir à la forme algébrique. Et ta réponse est fausse.

[Pseuda]

Non ? Le triangle peut être rectangle sans être rectangle isocèle ?

Comme dit Chan, il y a une infinité de solutions pour chaque équation (enfin je pense, je n'en ai résolue qu'1 sur les 3).

[musique137]

Bonjour,

Merci à tous pour vos réponses.

Je n'ai pas bien compris si je devais résoudre z² - z = ± i ( z^3 - z ) ou pas dans le cas où le triangle n'est pas isocèle. Et pourquoi il y a une infinité de solution ? Merci

[zygomatique]

je ne sais pas pourquoi on parle de triangle isocèle

si u et v sont deux vecteurs d'affixes a et b alors (u, v) = arg (b/a)

en l'appliquant ici on cherche donc quand/si arg[(z^3 - z)/(z^2 - z)] = +- pi/2

(et évidemment il y a deux autres égalités ...)

[Pseuda]

Bonjour,

Merci à tous pour vos réponses.

Je n'ai pas bien compris si je devais résoudre z² - z = ± i ( z^3 - z ) ou pas dans le cas où le triangle n'est pas isocèle. Et pourquoi il y a une infinité de solution ? Merci

Bonjour,

Je me suis mal exprimée, je reprends. Il ne faut pas résoudre cette équation (erreur de Carpate). Il faut faire comme tu as dit : le triangle M1M2M3 est rectangle en M1 ssi Z= est imaginaire pur, donc ssi il est égal à l'opposé de son conjugué () (après simplification bien sûr de Z).

Si tu as vu l'équation d'une droite ou d'un cercle à l'aide des complexes, ok, sinon, passe alors les complexes dans leur expression algébrique.

[zygomatique]

(z^3 - z)/(z^2 - z) = z + 1 ...

[musique137]

Merci à tous.

Donc si j'ai bien suivi j'obtiens (dans le cas où le triangle M1M2M3 serait rectangle en M1) :

Z=(z^3 - z)/(z^2 - z) = z + 1 = a + 1 + ib.

- Z barre = - ( a + 1 - ib ) = - a - 1 + ib.

Donc Z est différent de l'opposé de son conjugé. Ainsi le triangle M1M2M3 ne peut pas être rectangle en M1 ?