Puissance des nombres complexes et angle droit

[zygomatique]

pourquoi passer par la forme algébrique ?

en notant z* le conjugué de z

z + 1 est imaginaire pur <=> z + 1 = -z* - 1 <=> z + z* = -2

or z + z* = ... donc z = ... ?

[Pseuda]

Merci à tous.

Donc si j'ai bien suivi j'obtiens (dans le cas où le triangle M1M2M3 serait rectangle en M1) :

Z=(z^3 - z)/(z^2 - z) = z + 1 = a + 1 + ib.

- Z barre = - ( a + 1 - ib ) = - a - 1 + ib.

Donc Z est différent de l'opposé de son conjugé. Ainsi le triangle M1M2M3 ne peut pas être rectangle en M1 ?

Bonsoir,

Tu n'as pas compris la démarche. Il faut raisonner par équivalences, pour déterminer l'ensemble des complexes z tels que le triangle soit rectangle en M1 (qui doit être une condition nécessaire et suffisante d'appartenance) :

M1M2M3 est rectangle en M1 ssi ....(équation d'inconnue z).... ssi .....(équation arrangée et simplifiée) .... ssi z = ...

[musique137]

pourquoi passer par la forme algébrique ?

en notant z* le conjugué de z

z + 1 est imaginaire pur <=> z + 1 = -z* - 1 <=> z + z* = -2

or z + z* = ... donc z = ... ?

Je comprends mieux la démarche maintenant.

Donc z + z* = -2 or z + z* = 2a donc z = -1.

Est-ce juste ?

[Ben314]

Que tu passe par la forme algébrique ou pas, ça ne change quasiment rien au problème et ça donne évidement la même solution.
Le tout c'est uniquement de ne pas écrire d'énorme conneries :

Donc si j'ai bien suivi j'obtiens (dans le cas où le triangle M1M2M3 serait rectangle en M1) :
Z=(z^3 - z)/(z^2 - z) = z + 1 = a + 1 + ib.
- Z barre = - ( a + 1 - ib ) = - a - 1 + ib.
Donc Z est différent de l'opposé de son conjugé. Ainsi le triangle M1M2M3 ne peut pas être rectangle en M1 ?

Là, le truc en rouge est complètement faux vu que la ligne juste au dessus tu as écrit que Z est égal à l'opposé de son conjugué lorsque a+1+ib=-a-1+ib, c'est à dire lorsque 2a=-2, c'est à dire a=-1 (et b quelconque).
Il y a donc une infinité de solution, à savoir tout les z=-1+ib avec b quelconque.

Donc z + z* = -2 or z + z* = 2a donc z = -1.
Est-ce juste ?

Ben non. Si 2a=-2, tout ce que ça te dit, évidement, c'est que a est égal à -1 et surement pas que a+ib est égal à -1.
De nouveau, ça te dit que z=-1+ib avec b quelconque.

[musique137]

Bonjour,

Un grand merci à tous de m'aider car j'ai du mal avec la manipulation des nombres complexes.

J'ai essayé de faire le cas où le triangle M1M2M3 est rectangle en M2.

Donc les vecteurs M2M1 et M2M3 sont orthogonaux et le nombre complexe Z est un imaginaire pur.

Z =(z^3 - z²) / (z - z²) = (z² - z) / (1 - z) = - z.

En notant z* le conjugué de z on veut :

Z = Z*
- z = - (-z) *
z = (-z)*
a + ib = -a + ib
2a = 0
a = 0

Donc le complexe z cherché est z = ib avec b quelconque.

[Pseuda]

Bonsoir,

Ok c'est ça. On a : z=-z*, donc z est un imaginaire pur, de la forme ib, avec b réel.

[Lostounet]

Enfin un avatar, Pseuda hahaha!
J'aime bien

[Pseuda]

C'est un lapin crétin, j'adore.

Le tien aussi a changé. Question indiscrète : C'est toi ?

[Lostounet]

La réponse par MP :p

[musique137]

Bonsoir,

Merci pour la réponse. Ensuite dans le cas où le triangle est rectangle en M3 j'ai fais :

Z = z² - z^3 / z - z^3 = z / z +1.

Z = - Z*
z / z +1 = - ( z* / z* +1)
z + 2 z z* + z* = 0.
2a +2a² +2b² = O

Ainsi a = b = 0 et z = 0.

[Pseuda]

Bonsoir,

Ca va jusqu'à a²+b²+a=0, mais ceci ne se résout pas en a=b=0.

Tu peux chercher l'ensemble des couples (a,b) qui vérifient a²+a+b²=0, a0, avec le delta du polynôme du 2nd degré. Cela donne une condition sur b, puis les solutions.

[musique137]

Bonsoir,

Merci Pseuda.

J'ai fais : a + a² + b² = O avec delta = 1 - 4b².

Si b = ± 1/2 alors delta = O et la seule solution est a = -b / 2a = ± 1/4. Cette solution de fonctionne pas.

Ensuite il faut traiter le cas du discriminant positif, soit b <± 1/2. Mais après je ne sais pas comment faire pour trouver les solutions.

[Ben314]

On va encore dire (à juste titre...) que je ne fait que râler... mais, je trouve que, face à l'équation a+a²+b²=0 il faut quand même être un peu vicieux pour chercher à exprimer en fonction de (=équation du second degré) plutôt que en fonction de (=immédiat...)

Et sinon, pour ne pas faire que râler, je proposerais bien de récrire a+a²+b²=0 sous la forme (a+1/2)²+b²=(1/2)² vu que c'est l'équation d'un . . .

[Pseuda]

On va encore dire (à juste titre...) que je ne fait que râler... mais, je trouve que, face à l'équation a+a²+b²=0 il faut quand même être un peu vicieux pour chercher à exprimer en fonction de (=équation du second degré) plutôt que en fonction de (=immédiat...)

Et sinon, pour ne pas faire que râler, je proposerais bien de récrire a+a²+b²=0 sous la forme (a+1/2)²+b²=(1/2)² vu que c'est l'équation d'un . . .

Bonjour,

Hum oui (j'y ai pensé en me retournant dans mon lit cette nuit). Comme quoi le choix de (a,b) au lieu de l'habituel (x,y) peut induire en erreur.

Donc @musique137, avec l'habituel (x,y), M1M2M3 est rectangle en M3 ssi (x+1/2)²+y²=(1/2)² . On reconnaît l'équation de quoi ?

Bonnes fêtes de fin d'année à toutes et à tous !

[Carpate]

Pour finir l'année avec un peu de géométrie
rectangle en 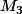: avec réel
soit (simplification légitime car les cas 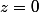et 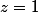correspondent à un triangle réduit à un seul point)
Soit A d'affixe -1, les vecteurs et sont orthogonaux.
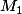décrit le cercle de diamètre AO, de centre et de rayon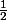

Bonne année à tous