Produit scalaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
analysis
- Messages: 2
- Enregistré le: 18 Juin 2014, 15:10
-
 par analysis » 18 Juin 2014, 15:12
par analysis » 18 Juin 2014, 15:12
Bonjour,
je cherche à construire un produit scalaire pour lequel deux vecteurs u,v par ex (1;2) et (3;1) formeraient une base othonormée.
Je dois donc me servir de la définition d'un produit scalaire, cad forme, bilinéaire et symétrique. Je sais aussi que =0. Je peux également me servir de la norme de mes vecteurs qui doit valoir 1.
Mais pour construire un produit scalaire qui respecte ces conditions, je ne sais pas vraiment comment m'y prendre. Pourriez-vous m'aider svp ?
Merci d'avance.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Juin 2014, 05:20
par zygomatique » 20 Juin 2014, 05:20
salut
un produit scalaire est une forme bilinéaire symétrique que tu peut représenter par la matrice
)
tu as trois inconnues ... et trois informations ....
ça devrait le faire ....
:lol3:
ou encore
si
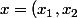 \ et \ y = (y_1, y_2))
alors ton produit scalaire s'écrit

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
analysis
- Messages: 2
- Enregistré le: 18 Juin 2014, 15:10
-
 par analysis » 21 Juin 2014, 11:48
par analysis » 21 Juin 2014, 11:48
En fait j'ai réussi à résoudre cet exercice entre temps, mais merci beaucoup pour votre aide :)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 21 Juin 2014, 12:44
par zygomatique » 21 Juin 2014, 12:44
et comment tu as fait ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Juin 2014, 13:26
par Ben314 » 21 Juin 2014, 13:26
Salut,
Sinon il y a une méthode trés "concon" : si on considère l'unique endomorphisme

tel que
=e_1)
et
=e_2)
où
)
est la base canonique, il est clair que la forme

défini par
=)
donne le résultat demandé (où

est le produit scalaire usuel).
Si tu réfléchi 15 seconde, ça te donne la matrice (symétrique)

du produit scalaire

en fonction de la matrice de passage (inversible)
)
de la base canonique à la base
)
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
