Produit de Cauchy
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Charmander
- Membre Naturel
- Messages: 90
- Enregistré le: 13 Oct 2013, 16:22
-
par Charmander » 27 Fév 2015, 12:38
Bonjour,
Un petit détail dans le produit de Cauchy me perturbe:
On sait que si
=\sum_{k=0}^{+\infty}a_k x^k)
=\sum_{k=0}^{+\infty}b_k x^k)
alors
b(x)=\sum_{n=0}^{+\infty}(\sum_{k=0}^{n} a_k b_{n-k})x^n)
Mais comment on fait si par exemple, b ne commence pas à l'indice 0 mais à l'indice 1 ?
=\sum_{k=1}^{+\infty}b_k x^k)
On pourrait poser
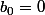
et simplifier après, mais si j'ai l'impression que ça donne pas le même résultat.
Notamment, il me semble que
b(x)\neq\sum_{n=0}^{+\infty}(\sum_{k=1}^{n} a_k b_{n-k})x^n)
Ca doit être un petit détail mais ça me perturbe énormément.
Merci d'avance pour vos explications.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 27 Fév 2015, 12:53
Bonjour,
A ta place, si l'indice commence par
, j'aurai factorisé la série par
, et donc, j'aurai une série de la forme :
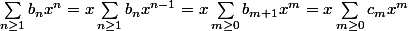
, en posant :
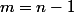
et
, pour tout :
.
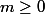
Cordialement. :happy3:
-
Charmander
- Membre Naturel
- Messages: 90
- Enregistré le: 13 Oct 2013, 16:22
-
par Charmander » 27 Fév 2015, 13:13
Bonjour,
Merci pour votre réponse, mais en fait, j'ai envie de relier
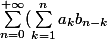x^n)
à
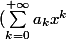(\sum_{k=1}^{+\infty}b_k x^k))
Or si je fais votre méthode, je trouve
b(x)=\sum_{n=0}^{+\infty}(\sum_{k=0}^{n} a_k b_{n-k-1})x^{n+1}<br />=\sum_{n=1}^{+\infty}(\sum_{k=0}^{n-1} a_k b_{n-k-1})x^{n})
Il y a donc un problème d'indice dans la somme intérieure... Je ne pourrai jamais faire apparaître les termes symétriques k et n-k sans faire apparaître des -1 +1. :triste:
Comment continuer ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 27 Fév 2015, 13:19
Les termes symétriques sont les
 = (q,p))
tels que :
si j'admets que ton calcul ne contient d'erreurs à une certaine étape, non ? J'ai pas vérifié ton calcul. :happy3:
-
Charmander
- Membre Naturel
- Messages: 90
- Enregistré le: 13 Oct 2013, 16:22
-
par Charmander » 27 Fév 2015, 13:35
Il y a probablement une erreur (de frappe ou de calcul) quelque part... Tant pis je laisse tomber vaut mieux en discuter avec un crayon et un papier, c'est trop galère de tout taper sur LateX :hein:
-
Escargot92
- Membre Naturel
- Messages: 11
- Enregistré le: 12 Mai 2014, 11:25
-
par Escargot92 » 27 Fév 2015, 13:46
b n'est pas supposé avoir un indice positif? car pour la premiére itération t'as n=0 et k=1 ce qui fait
.
Sinon pourquoi tu ne commence pas par n=1 et k=1 avec une certaine constante:
b(x) = S_{0}+\sum_{n=1}^{+\infty}(\sum_{k=1}^{n} a_k b_{n-k})x^n)
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
par SLA » 27 Fév 2015, 15:18
Charmander a écrit:Bonjour,
Un petit détail dans le produit de Cauchy me perturbe:
On sait que si
alors
Mais comment on fait si par exemple, b ne commence pas à l'indice 0 mais à l'indice 1 ?
On pourrait poser
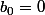
et simplifier après, mais si j'ai l'impression que ça donne pas le même résultat.
Notamment, il me semble que
Ca doit être un petit détail mais ça me perturbe énormément.
Merci d'avance pour vos explications.
Salut!
Je dirais tout simplement que ton problème vient du fait que dans
si
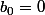
alors
et tout marche!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
