Produit de Cauchy
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 01 Déc 2013, 20:54
par psp » 01 Déc 2013, 20:54
Bonsoir,
On pose f de rayon de convergence 1 développable en série entière en 0 tel que
= \bigsum_{n=0}^{\infty} a_{n}z^{n})
Je dois déterminer pour

et
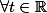
le résultat de
^{2}|)
. J'utilise le produit de Cauchy mais je ne tombe pas sur l'expression du livre,
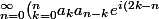t})r^{n})
, comment faire pour retomber sur cette formule ?
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 01 Déc 2013, 21:02
par jlb » 01 Déc 2013, 21:02
psp a écrit:Bonsoir,
On pose f de rayon de convergence 1 développable en série entière en 0 tel que
= \bigsum_{n=0}^{\infty} a_{n}z^{n})
Je dois déterminer pour

et
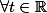
le résultat de
^{2}|)
. J'utilise le produit de Cauchy mais je ne tombe pas sur l'expression du livre,
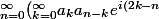t})r^{n})
, comment faire pour retomber sur cette formule ?
f est à coefficient réel? sinon ta 2ème somme s'arrête à n et pas à infini!!
tu calcules f(z).(f(z)barre) avec produit de Cauchy et tu as ton résultat
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 01 Déc 2013, 21:25
par psp » 01 Déc 2013, 21:25
Je te présente mes excuses tu as raison :marteau:
J'ai trouvé merci
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 01 Déc 2013, 21:43
par psp » 01 Déc 2013, 21:43
A-t-on le droit d'intégrer une telle expression ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Déc 2013, 22:13
par Ben314 » 01 Déc 2013, 22:13
psp a écrit:A-t-on le droit d'intégrer une telle expression ?
Tu veut intégrer par rapport à quoi ?
Si c'est par rapport à r, ta question revient à "A-t-on le droit d'intégrer une série entière" et tu doit connaitre la réponse.
Si c'est par rapport à t, il faut revenir au chapitre précédent (je pense...) : quelle est la condition la plus fréquente qu'on utilise pour permuter un symbole
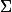
et un symbole

?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 02 Déc 2013, 00:25
par deltab » 02 Déc 2013, 00:25
Bonsoir.
N'y a-t-il par une erreur dans le produit de Cauchy de
 \times \overline{f(z)}=(\sum_{n=0}^{\infty} \text{ }a_nz^n)(\sum_{n=0}^{\infty} \text{ }\overline{a_nz^n}))
.
De plus dans l'énoncé, il n'est pas précisé que les

sont réels, on n'a donc pas
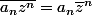
.
Pour
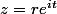
, on aura:
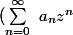(\sum_{n=0}^{\infty} \text{ }\overline{a_nz^n}) \text{ }= \text{ }\sum_{n=0}^{\infty}\left(\sum_{k=0}^{n}\text{ } a_k e^{ikt}r^k \text{ }\overline{a_{n-k}e^{i(n-k)t}r^{n-k}})\right))
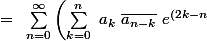it} \right)\text{ }r^n)
-
psp
- Membre Relatif
- Messages: 312
- Enregistré le: 23 Oct 2007, 14:35
-
 par psp » 02 Déc 2013, 23:10
par psp » 02 Déc 2013, 23:10
Ben314 a écrit:Tu veut intégrer par rapport à quoi ?
Si c'est par rapport à r, ta question revient à "A-t-on le droit d'intégrer une série entière" et tu doit connaitre la réponse.
Si c'est par rapport à t, il faut revenir au chapitre précédent (je pense...) : quelle est la condition la plus fréquente qu'on utilise pour permuter un symbole
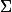
et un symbole

?
Convergence uniforme de la série, c'est le cas puisque
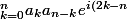t})
est bornée et

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
et
le résultat de
. J'utilise le produit de Cauchy mais je ne tombe pas sur l'expression du livre,
, comment faire pour retomber sur cette formule ?
et un symbole
?