Produit de cauchy

[Anaisdeistres]

Bonjour,
Je suis en L2 Maths et je cherche à résoudre un exercice.

1. Etudier la convergence simple sur R de la série de fonctions ? fn où n∈N
les fonctions fn sont définies par : quelque soit quelque soit

q1 ok

2. Etudier la série produit de Cauchy de par elle-même pour avec

Est-ce-que ?

Et du coup on fait la limite de de ?

Merci

[jlb]

Salut, personnellement, ton énoncé, cela semble deux questions totalement indépendantes!!

Tu dois calculer pour la question 2)

[mathelot]

bonsoir,
est ce que tu as vu que je t'avais calculé une somme (dans un autre thread resté sans réponse) ?

[mathelot]

est la dérivée de

on va étudié la convergence de la série des primitives de f_n


on a donc à étudier la somme de termes d'une progression géométrique

[Anaisdeistres]

A oui pardon je parlais du point 2 pour le point 1 je l'ai fait j'ai trouver
si alors lorsque donc la série diverge
si alors lorsque donc la série converge
si alors lorsque donc la série converge

[infernaleur]

A oui pardon je parlais du point 2 pour le point 1 je l'ai fait j'ai trouver
si alors lorsque donc la série diverge
si alors lorsque donc la série converge
si alors lorsque donc la série converge

Il y a plusieurs erreurs :
(1) donc tend vers pas !!

(2)Quand tu as une série de terme général une suite , ce n'est pas parce que la suite tend vers que la série converge, le premier contre exemple que tu as du voir est la série harmonique () on a bien que , mais la série diverge.

[infernaleur]

Sinon pour montrer la convergence d'une série tu as plusieurs méthodes :

Méthode 1: (convergence absolue)

Si à partir d'un certain rang. Et si la série de terme général converge.
Alors la série de terme général converge absolument et donc converge.

Exemple : on étudie la série de terme général (pour n plus grand que 1)
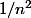
Comme . Et comme il est connu que la série de terme général converge, bha la série de terme général converge.

Méthode 2: (critère pour les séries à termes positifs)

Soit une suite positif à partir d'un certain rang.
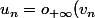Si (si la suite est "dominé" par ).
Si la série de terme général converge.
Alors la série de terme général converge .

Exemple :
Soit un réel fixé.
On prend

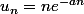
On voit immédiatement que si , alors . Donc la série de terme général diverge grossièrement.

Si :
.
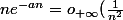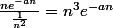
En effet, pour n non nul : et cela tend vers 0 par croissance comparée.
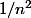
Donc on en déduit, comme est une suite positif et que la série de terme général converge, que la série de terme général converge aussi.

Voila j'ai pas listé toutes les méthodes possibles attendu en L2 (critère de d'Alembert, de Cauchy ...). Mais pour moi, je pense que c'est deux méthodes sont les plus fréquentes et qu'il faut parfaitement les maitriser.

[mathelot]

Question (2)
Calculons au carré.
Le terme général du carré (produit de Cauchy) est


si (a_n) est une progression géométrique de raison q et de premier terme 1, il vient


d'où

or

[Anaisdeistres]

Je corrige la q1



~ CV d'après le théorème de Riemann donc CV



e^{0}=1 et ne^{-nx}=n DV donc ne^{-nx} DV



~ CV d'après le théorème de Riemann donc CV

q2 ok merci

[mathelot]

Je corrige la q1



~ CV d'après le théorème de Riemann donc CV

si x<0 la suite ne tend pas vers zéro et la série diverge


e^{0}=1 et ne^{-nx}=n DV donc ne^{-nx} DV



~ CV d'après le théorème de Riemann donc CV

je n'ai pas compris

q2 ok merci

[Anaisdeistres]

je comprend pas ce que c'est merci

[mathelot]

zut, je fais du hors-programme

veut dire dérivée de f par rapport à la variable réelle q.

[jlb]

……………..
d'où

or

Bonsoir, pourquoi tu ne conclus pas directement à , puisque ?

[mathelot]

……………..
d'où

or

Bonsoir, pourquoi tu ne conclus pas directement à , puisque ?

parce que il y a une formule qui m'intrigue; la série S vérifie

[jlb]

Oui car S² = (-1 + S)' s'écrit aussi S² = S'?

[jlb]

Je corrige la q1



~ CV d'après le théorème de Riemann donc CV



e^{0}=1 et ne^{-nx}=n DV donc ne^{-nx} DV



~ CV d'après le théorème de Riemann donc CV

q2 ok merci

Bonsoir, tu as l'air d'être perdue entre les x et les n! L'aide t'a été utile ou tu as des questions. J'ai encore 10min devant moi.

[Anaisdeistres]

oui c'est bon pour moi j'ai compris pourquoi enfête on a juste fait la dérivée de l'expression

[Anaisdeistres]

Je corrige la q1



~ CV d'après le théorème de Riemann donc CV



e^{0}=1 et ne^{-nx}=n DV donc ne^{-nx} DV



~ CV d'après le théorème de Riemann donc CV

q2 ok merci

Bonsoir, tu as l'air d'être perdue entre les x et les n! L'aide t'a été utile ou tu as des questions. J'ai encore 10min devant moi.

Non cava aller merci beaucoup bonne soirée

[jlb]

Ok, du coup

Et le d/dq signifie que tu dérives l'expression par rapport à la variable q: on pourrait écrire (x^{n+1})' = (n+1)x^{n} sous la forme d/dx (x^{n+1})


Mais pour avoir droit de faire cela, il ya des conditions à vérifier et si tu ne connais pas ce théorème , oublie vite cela!!

[Anaisdeistres]

oui merci