Série produit de Cauchy

[Maths-ForumR]

Bonjour,
J'ai du mal a résoudre cet exercice :

1) On veut montrer la convergence de la série bn
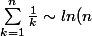1)a. En utilisant , déterminer la limite de bn
1)b. Déterminer le signe de |bn | - |bn+1 | quand n>= 3 et conclure



Déterminer la somme de la série bn

JE n'arrive pas a démarrer l'exercice
Pouvez vous m'aider
Merci d'avance

[Razes]

Calcule et simplifie l'expression.

[Maths-ForumR]

Très bien merci

Donc ak.a(n-k) =

donc bn =

[Razes]

Très bien merci

Donc ak.a(n-k) =

donc bn =

c'est bon, le reste n'est pas bon. Tu peux sortir car il ne dépend pas de .

Tu as:

[Maths-ForumR]

Ah donc

bn =]

[Razes]

Le dernier terme est facile à calculer avec un changement d'indice ou essais d'écrire les premiers et less derners de la somme pour voir.

[Maths-ForumR]

J'ai du mal avec les changement d'indice si on pose l=n-k

alors le dernier terme devient : Somme (de 1 à ? ) de 1/l ?

[Razes]

Le dernier terme est facile à calculer avec un changement d'indice ou essais d'écrire les premiers et les derniers de la somme pour voir.

[Maths-ForumR]

ça donne 1+1/2+1/3+ ... + 1/(n-3) + 1/(n-2) + 1/(n-1) = ?

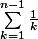
[Razes]

C'est bon. Tu reporte la valeur dans ton expression.

[Maths-ForumR]

On a donc bn

Et est-ce juste si je dis lim l bn l = 0 donc lim bn = 0 ?

Ensuite j'ai fais la question 1)b.

Mais je suis bloqué a la question 2)

[Razes]

Oui, c'est juste:

Pour écrire tape le code +\infty

[Maths-ForumR]

Très bien merci

Pour la question 2) il faut que j'utilise l'équivalent trouvé de bn ?
Je dois faire le lien ente bn et ln (1+x) ?

[Razes]

C'est quoi ?

[Maths-ForumR]

Dans mon exercice Un correspond a bn

[Razes]

Critères de convergence "Théorème d'Abel".
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_d%27Abel_(analyse)

[Maths-ForumR]

merci pour le lien je pense donc que c'est plutôt an qui joue le rôle de Un et on a le même résultat que l'exemple 1 à savoir ln(2)

Mais du coup pour calculer la somme de bn a t-on :