Problème ouvert

[sarah2811]

Bonjour, voici l'énoncé :

Démontrer que pour tout entier n tel que n≥3, on peut trouver n entiers strictement positifs x1,x2,...xn distincts deux à deux qui vérifient :
1/x1+1/x2+...+1/xn = 1

Quelqu'un pourrait m'aider? Merci

[Ben314]

Salut,
On peut tout faire en partant de l'unique constatation que

etc...

et il y a de très nombreuses autres solutions avec la même idée, par exemple écrire que

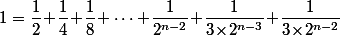
La somme des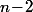 premier donne bien sûr et les deux derniers donnent

[nodgim]

Ou encore : 1 = 1/2 + 1/ 2 avec le 2ème 1/2 :
1 / 2 - 1 / 3 = 1/6 ...........................d'où 1 = 1/2 + 1/3 + 1/6
1/6 - 1/7 = 1/42.............................d'où 1 = 1/2 + 1/3 + 1/7 + 1/42
1/42-1/43 = 1/1806...................d'où 1 = 1/2 + 1/3 + 1/7 + 1/43 + 1/1806
.......

[Ben314]

Questions subsidiaires :
- Montrer que pour un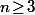 fixé, il y a un nombre fini 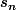de solutions (jusque là, c'est facile).
- Y-a-t-il des méthodes (relativement) simple de calcul de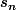 ? (là, j'ai pas trop réfléchi à la question...)