Problème ouvert ? 2^n et 3^m

[Ben314]

Si j'ai tout bien compris la méthode "doraki" (j'ai pas fait exactement pareil) :

R0= "dernier chiffre entré=0 ET dernière retenue=0"
R1="(dernier chiffre entré=0 ET dernière retenue=1)OU BIEN(dernier chiffre entré=1 ET dernière retenue=0)"
R2= "dernier chiffre entré=1 ET dernière retenue=1"

Edit : je vient de comprendre... pourquoi c'était pas clair pour moi : je continuais à raisoner avec 3a=2a+a et "mes retenues" étaient celles que l'on obtient dans l'addition 2a+a.
Doraki étant beaucoup plus fort en calcul que moi, il ose calculer directement 3a en faisant... 3 fois a, c'est vachement plus balèse !!!! :zen:

[Doraki]

Oui, puisque l'algo d'addition de x avec 2x consiste à faire (chiffre à écrire + 2*prochaine retenue) = prochain chiffre entré + (dernier chiffre entré + retenue) , donc autant ne se souvenir que de la somme (dernier chiffre entré + retenue).
(qui correspond à la retenue quand on fait l'algo de calcul de 3*x)

Sinon, je suis d'accord, ça ne prouve à peu près rien, à part que quand on regarde ce qui se passe concrètement et qu'on se dit "tiens la proportion a l'air de tendre vers environ 1/2", ça permet de se donner une pseudo-justification qui dit que le plus vraisemblable est que oui ça tend vers 1/2.

[busard_des_roseaux]

moi aussi, je viens de comprendre :id:

ceci dit, je trouve ça extra !! car:

i) il me semble que l'automate de Doraki n'est pas probabiliste mais mécanique ?

ii) on n'a qu'à l'initialiser avec
(base 2)

er récurrer
??

si son algorithme est bien mécanique et non probabiliste,
on a résolu (un petit bout ) d'un problème ouvert que je vous exposerai...

parce que avec ça, on peut regarder l'évolution de la proportion des 1
dans la récurrence ??

[Doraki]

Je l'initialise avec 1, moi =)

Mais n'empêche que tout le raisonnement que j'ai fait avec part de "on prend une suite de chiffres aléatoires" et je vois pas trop comment vraiment formaliser mon truc encore.

[Ben314]

Sauf erreur, l'algo de Doraki peut parfaitement être vu comme "non probabiliste" : c'est d'ailleur l'algo que l'on voit au primaire pour faire des multiplications et, A MON EPOQUE, on l'enseignait sous forme trés déterministe, peut être que ça a changé depuis... :doh:
Sous la forme "déterministe", il calcule effectivement les 0/1 de 3^(n+1) en connaissant ceux de 3^n mais pas le nombre de 1 de 3^(n+1) en fonction de celui de 3^n...

[nodjim]

3^n ne serait il pas un nombre univers, par hasard ?

[nodjim]

si son algorithme est bien mécanique et non probabiliste,
on a résolu (un petit bout ) d'un problème ouvert que je vous exposerai...

Du syracuse ?

[Doraki]

3^n ne serait il pas un nombre univers, par hasard ?

Si la période de la suite ((3^n) mod 2^k) est du style 2^(k-a) pour k assez grand, alors je pense que la réponse a la question que tu as presque posée est oui.

edit : et ça l'est avec a=2.

[busard_des_roseaux]

On se donne une proportion de 1, p. (La proportion de 0 est alors q = 1-p).
On calcule la proportion de chaque état R0, R1, R2 à l'aide d'un système.

P(R0) = q²/(q²+pq+p²)
P(R1) = pq/(q²+pq+p²)
P(R2) = p²/(q²+pq+p²)

vous pourriez expliquer ? je ne comprends pas :hum:

(je vais lire ça en attendant qu'ils reviennent )

[Ben314]

Doraki considère que le système est stable, c'est à dire que les proba r0, r1 et r2 des états R0, R1 et R2 sont les mêmes à chaque étapes.

Par exemple, comme l'état R1 provient soit de R0 -1 soit de R2 -0, on a :
r1 = p r0 + q r2
idem pour r0 et r2 cela donne un système (lié) auquel il faut adjoindre r0+r1+r2=1 pour obtenir les solutions.

[Doraki]

En fait on fait une expérience en prenant une suite de variables aléatoires (les chiffres) qui valent 1 avec proba p et 0 avec proba (1-p), et qu'on donne à manger une par une à l'automate, et on regarde quel est le comportement de l'automate et ce qu'il donne en sortie.

En partant de l'état initial R0,
et en appliquant la transition 0 avec propbabilité (1-p), et la transition 1 avec la probabilité p, on peut regarder la probabilité Pn(Ri) d'être à l'état Ri après n transitions.
On regarde les triplets (Pn(R0), Pn(R1), Pn(R2)) .
n=0 : (1,0,0)
n=1 : (1-p,p,0)
n=2 : ((1-p),p(1-p),p²)
etc.

En fait, on constate que la suite des triplets (Pn(R0), Pn(R1), Pn(R2)) (i.e. la loi de la variable aléatoire En = "état après n transitions"), a une limite, que l'on peut déterminer en disant que à partir de cette loi limite et en appliquant les transitions (de manière probabiliste), on retombe sur la même loi.

Cette loi limite donne en quelque sorte la fréquence d'apparition de chaque état lors du parcours d'une suite aléatoire de chiffres 0 et 1.
Le deuxième calcul, je pense qu'il doit correspondre à .. euh.. la valeur de la limite (qui existe presque surement) de la proportion de 1 de la suite qu'on obtient en sortie.

[Ben314]

Au fait, j'ai pas bien compris vos référence à un "nombre univers" : ça doit pas avoir une infinité de chiffres aprés la virgule un "nombre univers" ?
Vous voulez "accoller" les chiffres des différents 3^n les uns derrières les autres (aprés la virgule) ?

Et ça :

Si la période de la suite ((3^n) mod 2^k) est du style 2^(k-a) pour k assez grand, alors je pense que la réponse a la question que tu as presque posée est oui.

J'ai pas bien vu le rapport avec le reste... (bien qu'effectivement je comprenne "l'edit" : comme 3 est d'ordre 2 modulo 2^3, il est d'ordre 2^(n-2) modulo 2^n)

[Doraki]

Ben ça doit impliquer que si tu commences à regarder à partir du 3ème chiffre, les séquences de k chiffres des nombres 3^n, on devrait avoir une suite périodique qui contient justement toutes les séquences possibles. Enfin j'crois.

[nodjim]

Ma question précise sur la qualité de nombre univers de 3^n est celle ci:
Soit n aussi grand que l'on veut, écrit en nombre binaire, existe t il toutes les séquences possibles de k bits, k donné ?
C'est un peu différent de la signification habituelle du nombre univers, étant donné que 3^n n'est pas infini.
La question la plus sensible est: peut on trouver une suite de 1 ou de 0 aussi longue que l'on veut ?

[busard_des_roseaux]

re-bonjour,

le souci, c'est que j'ai pas mal de taf aujourd'hui...
voilà des cogitations de la nuit

(binôme)
en divisant par 2^n


posons
c'est une famille de nombres décimaux de somme 1
(de nouveau, formule du binôme)



après , ce qui serait agréable, c'est de faire apparaitre une mesure
avec une densité sur [0;1] (en relation avec la limite des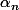 qui forment une sorte de partition de l'unité) et d'exprimer le nombre de digits à 1 de
avec une mesure à densité...
donc si (statistiquement) le nombre de digits à 1 de , donc la mesure de comptage des 1, était une mesure à densité
reliée à ou à la loi binomiale (??) , ça serait top.
j'avoue que ça me dépasse

[busard_des_roseaux]

re-bonjour,

voilà ce que je conjecture :doh:

les digits de ,base 2, ont une fonction de densité f(x)
qui est:

soit

ce qui donnerait une fonction de répartition


pour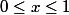

ou bien sa réciproque qui est aussi strictement croissante
de [0;1] sur [0;1] , je n'arrive pas à les distinguer dans les formules..

je suis persuadé que le nombre de 1 dans suit, asymptotiquement, une de ces deux lois de proba répertoriées. comment vérifier expérimentalement ?

[Doraki]

Je vois pas trop comment interpréter ce que t'as dit.
Les digits de 3^n c'est soit 0 soit 1, j'vois pas où peut intervenir une loi de densité là dedans :/

Sinon j'ai regardé pour n <= 10000, on dirait bien que si s(x) = somme des chiffres de x,


(ce à quoi on peut s'attendre si on considère que 3^n c'est log3/log2 chiffres pris au hasard entre 0 et 1)

[Ben314]

Bon, je comprend que dalle :

Si la question exacte est :

Soit n aussi grand que l'on veut, existe-t'il dans l'écriture binaire de toutes les séquences possibles de k bits ?

Alors la réponse est trivialement NON, vu que, dés que k dépasse (strictement) le nombre de chiffres de , et que la sequence commence par 1, il est clair qu'elle ne risque pas d'ètre une sous-séquence de !!!

Si la question exacte est :

Etant donné une séquence de k bits (binaire) fixée, existe t'il au moins un [respectivement une infinité] de n tels que cette séquence apparaisse dans l'écriture binaire de 3^n ?

Alors la réponse est (un peu moins trivialement) OUI :
Pour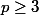 , 3 est d'ordre 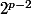modulo 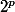ce qui signifie que l'ensemble des modulo 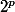(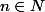) contient exactement le 1/4 des éléments de .
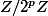Sauf que, si n est pair, se termine (en base 2) par 001 et, si n est impair, se termine par 011. Comme les éléments de 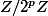se terminant par 001 ou 011 représentent le 1/4 du total, on en déduit qu'il sont tous des pour n bien choisi.
Conclusion : étant donée une séquence S (en binaire) quelconque, il existe une infinité de n tels que se termine par S001 (et une infinité se terminant par S011).

Dans les deux cas, je ne vois pas le rapport entre l'énoncé et le calcul du nombre de 1 dans l'écriture de en binaire.


Concernant ce qu'écrit busard_des_roseaux, je suis comme Doraji (encore !!!) : je vois pas bien de quelle "loi de densité" tu parle...

EDIT :
Je vient de voir une troisième possibilité :

Soient n et k fixés. Existe-t'il dans l'écriture binaire de toutes les séquences possibles de k bits ?

Là, clairement, la réponse dépend de k et n : pour k=1 et , c'est vrai ; pour n fixé et k "trop grand", c'est clairement faux.
On peut effectivement se poser la question pour k fixé et n "trés grand" : c'est effectivement pas évident...
Sauf que je vois toujours pas le rapport avec le nombre de 1 dans ...

[busard_des_roseaux]

Je vois pas trop comment interpréter ce que t'as dit.
Les digits de 3^n c'est soit 0 soit 1, j'vois pas où peut intervenir une loi de densité là dedans :/

Sinon j'ai regardé pour n <= 10000, on dirait bien que si s(x) = somme des chiffres de x,


(ce à quoi on peut s'attendre si on considère que 3^n c'est log3/log2 chiffres pris au hasard entre 0 et 1)

re,

on part du binome

on remarque que

on pose



les coefficients sont très réguliers, de somme 1.
possède environ digits

appelons moy(n) la moyenne des digits de ...



je me disais que l'on pourrait remplacer les coeff du binome par une gaussienne (on approche la loi binomiale par une loi normale) et la somme dans le log par une intégrale,
ce qui donnerait à la fois une densité et , expérimentalement, une valeur des termes suivants du développement asymptotique.


où (Bernoulli de paramètre )

je ne sais pas du tout où j'en suis ?? :doh:
c'est exact ? j'enfonce des portes ouvertes ?

[Doraki]

appelons moy(n) la moyenne des digits de ...

Euh mais.. si tu supposes de base que moy(n) = 1/2, c'est pas un peu de la triche et/ou faux ?
Même si on sait à quoi ressemblent les a(n,k), vu qu'ils passent à la moulinette à addition, j'vois pas trop comment ça pourrait donner des infos précises sur les chiffres de 3^n =/