Problème ouvert ? 2^n et 3^m

[busard_des_roseaux]

Bonjour,

je pense que le problème suivant est équivalent
à un problème ouvert:

Montrer que le nombre de digits non nuls , en base 2,
de tend vers l'infini avec l'entier .

ce qu'il y a comme formules

(trivial)
donc un shift gauche suivi d'une addition
et
(binome)
ce qui peut être vû comme le fait que l'on doit ajouter
digits de poids k,
(et évidemment effectuer les retenues, c'est là où le bat blesse)

@+

et aussi
(progression géométrique)

[ffpower]

Ca fait un moment que je voulais poster un topic la dessus ( bon moi je restais en base 10, mais ca doit revenir a peu près au même^^)

Donc ca tombe bien que tu aies fait ce topic..Je n'ai pour ma part trouvé aucune piste très interessante..

[nodjim]

Tiens! Je croyais que ce problème était résolu. C'est vraiment un problème ouvert ?

[busard_des_roseaux]

Tiens! Je croyais que ce problème était résolu. C'est vraiment un problème ouvert ?

vas-y , prouve qu'il est fermé , hihi :we:

[nodjim]

Je propose une vision de la progression du nombre de 1 dans 3^n en base 2, pas forcément une démo académique.
Quel que soit n, 3^n commence et finit par un 1. Si l'on pose que l'unité binaire est une distance, la vitesse de dilatation du nombre est > unité par opération. Par ailleurs il faut observer que, quand dans le nombre, il y a au moins 2 zéros successifs, un vide, on peut dire qu'on a affaire à 2 nombres différents qui progressent chacun indépendamment l'un de l'autre, celui en amont et celui en aval du vide.
Au fur et à mesure de la dilatation du nombre, on se trouve donc en présence d'îlots de nombres séparés par des vides et qui se dilatent chacun à la même vitesse. Les vides sont bouchés à l'aide de 1, et si pendant la dilatation, on crée des vides, ils se rebouchent.
Si l'on suppose une limite au nombre de 1, il faut alors supposer une proportion toujours plus faible des 1 par rapport au nombre de bits total, ce qui n'est pas compatible avec le scénario décrit.
Sinon, il semblerait que le nombre de 1 soit dans une proportion de 1/2 par rapport au nombre total de bits. Reste à savoir pourquoi...

[nodjim]

La preuve: on imagine un max de 1 atteint pour un 3^n0. Ce max est contenu dans un mot de k bits. Or, si on calcule les puissances de 3 modulo 2^k, le nombre 3^n0 reviendra périodiquement. Mais, par ailleurs, les puissances de 3 successives occupent toujours plus de bits, donc au moins un 1 supplémentaire sera trouvé après les k bits. Il ne peut donc y avoir de limite au nombre de 1.

[busard_des_roseaux]

Mais, par ailleurs, les puissances de 3 successives occupent toujours plus de bits, donc au moins un 1 supplémentaire sera trouvé après les k bits.

oui, mais le souci: imaginons que le nombre maximum de bits non nuls soient 4

3^3=11011

ça empêcherait pas d'avoir une suite de la forme
1010011
100100101
10100100001
10000100100001

le problème, c'est une numérotation de position.
si on intercale un grand nombre de zéros, même aléatoirement,
après un 1, ça fait tendre vers l'infini.

je suis quand même attentif à ta démonstration, l'idée repose sur le multinôme
(développement de )
mais comment se comportent les coeff binomiaux en base 2.
c'est probable qu'ils fournissent statistiquement un grand nombre de 1....

est-ce que l'on doit étudier le triangle de Pascal (coefficients du binome)
modulo 2 ou modulo 2^k , grâce au fait que l'addtion passe au quotient (au modulo) ?

[nodjim]

Apparemment, tu n'as pas saisi ce que j'ai écrit.
Si 3^3=11011, on retrouve ce "préfixe" 11011 avec 3^(3+8k).
Et c'est vrai pour tout n de 3^n.
OK ?

[busard_des_roseaux]

Apparemment, tu n'as pas saisi ce que j'ai écrit.
Si 3^3=11011, on retrouve ce "préfixe" 11011 avec 3^(3+8k).
Et c'est vrai pour tout n de 3^n.
OK ?

désolé, :hum: j'ai le sentiment que le problème est difficile..
peux tu indiquer une démonstration plus détaillée et plus formalisée ?

il faut montrer que le nombre de digits à 1 de 3^n en base 2
tend vers l'infini avec l'entier n...

si tu écris "on retrouve ce préfixe" 11011, je comprends qu'il existe une
suite extraite, qui contient au moins quatre 1 dans son écriture base 2.
on est loin de la conclusion attendue :hein:

quelque soit K, il existe N tel que
pour tout n >N , le nombre de digits non nuls de 3^n > K

[Doraki]

On sait qu'on a donc une séquence qui n'est pas bornée, mais ça veut pas dire qu'elle tend vers l'infini.

Sinon, il semblerait que le nombre de 1 soit dans une proportion de 1/2 par rapport au nombre total de bits. Reste à savoir pourquoi...

Statistiquement, si on prend un nombre aléatoire avec une proportion p de 1, qu'on le multiplie par 3, on obtient un nombre aléatoire avec une proportion p(2-3p+p²)/(1-p+p²) de 1. Et on observe que p = 1/2 est l'équilibre stable obtenu.
(j'ai pas réfléchi aux autres puissances/bases)

Donc oui il est très vraisemblable que la proportion de 1 tend vers 1/2.

[busard_des_roseaux]

Bonjour Doraki,

comment obtient-on cette proportion ?

le problème de la retenue est gérée avec les probas ?

ancienne retenue r=0 (avec proba 1-q)

r+0+0=0
r+1+0=1
r+0+1=1
r+1+1=0 --> r=1

nouvelle retenue r=1 en sortie avec proba (1-q)/4




ancienne retenue r=1 (avec proba q)

r+0+0=1
r+1+0=0 --> nouvelle retenue r=1
r+0+1=0 --> nouvelle retenue r=1
r+1+1=1 --> nouvelle retenue r=1

nouvelle retenue r=1 en sortie avec proba 3q/4


??

la probabilité d'une retenue passe , lors des additions successives
de q à
déja , je suis persuadé que cette suite de probabilités est chaotique

EDIT: en fait non, elle tend gentiment vers 0,5

[Doraki]

On a une retenue si un nombre aléatoire de k chiffres (avec la proportion de 1 qui vaut p) est supérieur à 2^k / 3.
De là on en déduit (sauf erreur de ma part) que la proportion/probabilité de retenue est p/(1-p+p²).

Mais en fait j'crois que j'me suis complètement gourré (des fois la retenue elle vaut 2 nan ? woops). Je referai tout ça quand j'aurai moins faim.

[nodjim]

[quote="Doraki"]On sait qu'on a donc une séquence qui n'est pas bornée, mais ça veut pas dire qu'elle tend vers l'infini.
QUOTE]

J'écris qu'il n'y a pas de limite, parce qu'on peut tjs ajouter au moins 1 à n'importe quel cardinal, ce n'est pas la définition de l'infini ?

[nodjim]

peux tu indiquer une démonstration plus détaillée et plus formalisée ?

Les valeurs des puissances successives de 3 modulo 2^k font partie d'un cycle fermé, puisque le nombre de valeurs possibles différentes est de 2^k max. Dans ce cycle, on peut choisir la valeur max qui donne le plus de 1 en base 2. Etc...
Je ne sais pas formaliser.

[Ben314]

Il me semble (comme Doraki) que tu montre seulement qu'il existe une sous suite extraite qui tend vers l'infini (ce qui est vrai mais... pas trés dur à montrer...)

[Doraki]

Bon j'ai refait mes calculs, et je redétaille :

La multiplication par 3 en base 2 correspond à un automate à 3 états R0,R1,R2 (la retenue peut valoir 0,1, ou 2) :

Par exemple, quand on est dans l'état R0 et qu'on lit un 1, on écrit un 1 et on passe à l'état R1

R0 -0-> 0, R0
R0 -1-> 1, R1

R1 -0-> 1, R0
R1 -1-> 0, R2

R2 -0-> 0, R1
R2 -1-> 1, R2.

On se donne une proportion de 1, p. (La proportion de 0 est alors q = 1-p).
On calcule la proportion de chaque état R0, R1, R2 à l'aide d'un système.

P(R0) = q²/(q²+pq+p²)
P(R1) = pq/(q²+pq+p²)
P(R2) = p²/(q²+pq+p²)

Ensuite on en déduit la proportion de 0 et de 1 dans la sortie du processus de multiplication par 3.
En particulier, p' = (2p-4p²+3p³)/(1-p+p²)
(donc je m'étais bien un peu gourré).
Et (p'-p)(1-p+p²) = p(1-p)(1-2p).
Donc p' = p lorsque p = 0, 1/2, ou 1.

J'imagine qu'on peut regarder la "stabilité" des solutions en regardant |dp'/dp| - 1 en ces trois valeurs.

[busard_des_roseaux]

je reprend l'idée de Doraki :we:

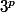
supposons que (une puissance de 3 quelconque "grande")
soit de poids fort et de plus , ait ses chiffres ,en base 2, au hasard.


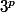
La proba que possède k chiffres 1 est de

(loi binomiale)

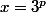
on multiplie par 3, écrit en base 2.



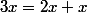
on fait donc un shift gauche sur les digits , suivi d'une addition.

lors de l'addition,
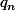
la probabilité d'une retenue vérifie la suite arithmético-géométrique
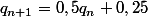
qui converge rapidement, au fil des additions, vers

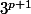
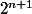
on en déduit que est de poids fort avec une proba , pratiquement de (en fait dans les )
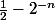
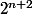
et de poids fort avec une proba quasiment de
(en fait dans les )

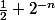
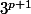
si est de poids fort
la proba qu'il posséde k digits à 1 passe de


à



à k fixé, cette proba tend vers zéro.

On en déduit que pour tout k, la proba que possède exactement k digits
à 1 tend vers 0 avec n.

ce qui indique de manière "heuristique" que le nombre de digits à 1 de tend vers l'infini avec n (si les 1 sont distribués
de manière aléatoire)

[Ben314]

En faisant le même calcul, je tombe sur le même p' que Doraki (je trouve ça... miraculeux !!!)
Par contre, je vois pas trop d'argument pour justifier l'idée proposée par Doraki ou busard_des_roseaux qui, il me semble, sous entendent une (relative) indépendance des positions de 1 dans l'écriture de 3^n en base 2.
Bon, évidement, il serait surprenant que ça ne soit pas du tout indépendant, mais n'empèche...

[busard_des_roseaux]

R2 -1-> 1, R2.

je ne comprends pas cette ligne :hein:
on utilise la distributivité de la multiplication par 3 (--> sur chaque digit ?)

avec une retenue de 2 et , ça fait 5 ?

combien d'entrées dans l'automate (deux opérandes ou une seule ??)

[Doraki]

oui il y a une seule entrée dans l'automate, on effectue la multiplication chiffre par chiffre.

Si t'as une retenue de 2 et que tu lis le chiffre 1, 2 + 3*1 = 5 = 1+2*2
Donc tu dois écrire un chiffre 1, et continuer avec une retenue qui vaut 2.