Probleme d'integrale(double, de surface,....)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
FreeDumz
- Membre Naturel
- Messages: 21
- Enregistré le: 19 Jan 2008, 17:54
-
 par FreeDumz » 09 Sep 2010, 08:21
par FreeDumz » 09 Sep 2010, 08:21
Salut a tous
J'ai passé mon examen de math hier, et il y a 3 question où je ne suis vraiment pas sur de mes reponses, si quelqun pouvait me dire si mon raisonnement est correcte, je lui en serais infiniment reconnaissant:
1) Calculer l'integrale double
xy dxdy
où (x,y)E R²|0=Alors là, j'ai fais la droite Y= X
ainsi que la droite Y+X=2
Donc j'obtenais 2 droites et j'ai pris mes bornes d'integration sur le triangle, ce raisonnement vous semble t'il correct?
2) Calculer L'integrale l sur le contour fermé
xy dx+x² dy
Donc integrale sur un contour fermé, j'ai de suite utiliser green
où l est le bord de la surface limitée par les courbes y=x² y=4
et comme borne d'integration, j'ai pris [-Sqrt(y), Sqrt(y)] et [0,4]
Merci d'avance pour vos reponses
3. Calculer le flux de F =(y²z,x+3z,z^3) à travers la surface intérieur de la sphère x²+y²+z²=1
Alors là, j'ai utilisé ostrogadsky, ce qui m'amène à faire l'integrale triple de:
3z²
Je passe en coordonnées sphérique avec:
X= R sin (phi) cos(teta)
Y= Rsin(phi) sin(teta)
Z= R cos (phi)
et le jacobien valant: R² sin(phi)
Donc pouvez vous me dire si ces raissonnement sont correctes
Merci d'avance
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 09 Sep 2010, 11:35
par Pythales » 09 Sep 2010, 11:35
Ca a l'air bon.
Juste une remarque au sujet de la 2 :
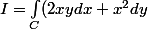-\int_C xydx)
et la 1ere est nulle, ce qui simplifie un peu le calcul
-
FreeDumz
- Membre Naturel
- Messages: 21
- Enregistré le: 19 Jan 2008, 17:54
-
 par FreeDumz » 09 Sep 2010, 13:18
par FreeDumz » 09 Sep 2010, 13:18
la premiere est nulle?
Je ne pense pas car si tu as viens le dessin, tu obtiens un triangle strictement postif donc ton integrale ne peut etre nul
Et pour la seconde, en utilisante green, il est beaucoup plus simple de la laisser sous sa premiere forme :)
Merci de ta reponses, j'ai le resultat demain
Je vous tiendrais au courant
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 09 Sep 2010, 15:01
par Pythales » 09 Sep 2010, 15:01
Quand je dis la 1ere est nulle, je parle de la 1ere intégrale de ma décomposition dans la question 2...
La formule de Grenn donne dans les 2 cas

qui est nulle par symétrie.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 94 invités
