Probabilité : Tirage
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sjfeg
- Messages: 8
- Enregistré le: 04 Déc 2013, 18:28
-
 par sjfeg » 07 Jan 2014, 12:11
par sjfeg » 07 Jan 2014, 12:11
Bonjour,
J'ai une urne avec
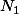
boules de couleur 1,
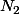
boules de couleur 2, ...,
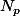
boules de couleur p.
Je tire sans remise jusqu'à l'obtention d'une couleur complète (ie j'ai tiré toutes les boules de la couleur). Quelle est la probabilité que j'ai obtenu la couleur k ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 07 Jan 2014, 12:48
par Sylviel » 07 Jan 2014, 12:48
Bonjour,
la question ne me semble pas simple (du moins je ne vois pas de solution simple).
Vient-elle d'un exercice ? Y a-t-il d'autres questions ?
En un mot est-on sûr que le problème a une "solution simple", ou suffit-il de proposer un calcul récursif / numérique ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
sjfeg
- Messages: 8
- Enregistré le: 04 Déc 2013, 18:28
-
 par sjfeg » 07 Jan 2014, 14:30
par sjfeg » 07 Jan 2014, 14:30
1) La question n'est pas issue d'un exercice, j'aurais du la poster dans la rubrique Café. Désolé :marteau:
2) S'il existe une expression formelle de la probabilité recherchée, elle m'échappe. Je cherche plutôt une formule de récurrence qui me permette de faire un calcul numérique.
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 07 Jan 2014, 16:26
par mrif » 07 Jan 2014, 16:26
sjfeg a écrit:1) La question n'est pas issue d'un exercice, j'aurais du la poster dans la rubrique Café. Désolé :marteau:
2) S'il existe une expression formelle de la probabilité recherchée, elle m'échappe. Je cherche plutôt une formule de récurrence qui me permette de faire un calcul numérique.
Une solution est d'introduire p variables aléatoires

où

correspond au nombre de tirages nécessaires pour obtenir la couleur complète i.
Les valeurs prises par

sont

où

La probabilité d'obtenir la couleur k sera
)
Il reste à trouver la loi de chaque

qui ne devrait pas être trop difficile.
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 07 Jan 2014, 17:27
par wserdx » 07 Jan 2014, 17:27
Je propose une formule qui me parait un peu monstrueuse mais peut-être accessible.
j'appelle
)
la probabilité qu'à la fin d'un tirage j'ai tiré exactement

boules de couleur 1 etc
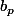
boules de couleur

.
Si je tire la couleur k complète, cela veut dire qu'au dernier tirage je tire une boule de couleur

, et j'ai tiré au plus

boules de couleur

et exactement

boules de couleur

.
La proba cherchée est donc
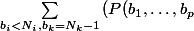/\sum_i{N_i-b_i})})
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 07 Jan 2014, 17:46
par wserdx » 07 Jan 2014, 17:46
La proba
)
peut s'exprimer ainsi:
/ C^{\sum_i{b_i}}_{\sum_i{N_i}})
-
sjfeg
- Messages: 8
- Enregistré le: 04 Déc 2013, 18:28
-
 par sjfeg » 07 Jan 2014, 21:20
par sjfeg » 07 Jan 2014, 21:20
D'accord sur la proba
)
. Pour la probabilité recherchée, le dénominateur n'est-il pas plutôt

?
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 07 Jan 2014, 21:36
par wserdx » 07 Jan 2014, 21:36
J'ai tiré

boules parmi les

, il en reste donc

. La probabilité de tirer la dernière boule de couleur

est donc

. On prend soin de prendre

ça peut donc se réécrire si tu veux

-
sjfeg
- Messages: 8
- Enregistré le: 04 Déc 2013, 18:28
-
 par sjfeg » 07 Jan 2014, 22:35
par sjfeg » 07 Jan 2014, 22:35
Exact :marteau:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Jan 2014, 17:33
par Ben314 » 09 Jan 2014, 17:33
Salut,
Aprés moult essais donnant des solutions assez compliquées, j'ai fini par trouver une formule pas trop compliquée.
La proba. que la première "couleur complète" obtenue soit la couleur 1 est :
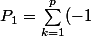^{k+1}\sum_{2\leq j_2<j_3<...j_k\leq p}\frac{N_1}{N_1+N_{j_2}+N_{j_3}+...N_{j_k}})
Par exemple, si l'urne contient

boules Rouges,

boules Vertes,

boules Bleues et

boules Jaunes (donc p=4 couleurs avec
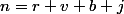
boules) alors la proba. que la première "couleur complète" obtenue soit Rouge est ;
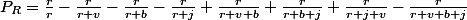
et je suis pas sûr qu'on puisse faire tellement plus simple comme formule...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
sjfeg
- Messages: 8
- Enregistré le: 04 Déc 2013, 18:28
-
 par sjfeg » 09 Jan 2014, 18:08
par sjfeg » 09 Jan 2014, 18:08
Merci à tous les 3 pour vos réponses :++:
Comme je m'intéresse à un modèle avec 6+ couleurs, j'ai pris la formule de wserdx qui se programme facilement avec quelques boucles imbriquées. :we:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Jan 2014, 13:31
par Ben314 » 11 Jan 2014, 13:31
sjfeg a écrit:Comme je m'intéresse à un modèle avec 6+ couleurs, j'ai pris la formule de wserdx qui se programme facilement avec quelques boucles imbriquées. :we:
Je sais pas trop comment tu programme pour trouver que la somme
wserdx a écrit:
qui contient

termes est plus "simple" que la somme
Ben314 a écrit:
qui elle ne contient que
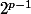
termes...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités