Probabilité de tirer la xième boule de l'urne A au nième tirage

[tsinapah]

Bonjour,

J'ai un petit (ptet pas tant que çà en fait, je ne sais pas trop...) problème de probas :

On dispose de 3 urnes A, B et C dont on tire des boules successivement et sans remise. Le choix de l'urne pour un tirage est équiprobable : on tire dans chaque urne indifféremment mais lorsqu'une urne est vide, elle est écartée. Ainsi si on a épuisé toutes les boules de C, il ne reste plus le choix qu'entre A et B.

Question : Quelle est la probabilité de tirer sa xième boule de A au nième tirage?

Je me casse le crâne depuis pas mal de temps là dessus mais çà ne vient pas, donc si quelqu'un a une idée... :happy2:

Merci d'avance

[tsinapah]

Peut être que pour simplifier, il faut commencer par chercher la probabilité qu'une urne donnée soit vide après n tirages? Mais bon déjà ca me parait chaud...

[alavacommejetepousse]

bonjour
combien de boules initialement dans A,B,C?

[Hydre]

Salut,
Quelques problèmes dans ton énoncé :
- cf la question de alavacommejetepousse (très bon pseudo pour être cité :p)
- si pas d'autres données, poser des nombres de boules pour chaque urne :

na = nombre de boules dans l'urne a
nb et nc idem

n = na+nb+nc
Soit P une mesure de probabilité.

P(tirer la première boule dans A) = na/n

P(tirer la 2ème boule dans A) = P(tirer la 2ème boule dans A sachant que la 1ere a été tirée dans A) + P(tirer la 2eme boule dans A sachant que la 1ere n'a pas été tirée dans A)
Après je pense qu'il faut utiliser la loi hypergéométrique (car tirage sans remise) ou bien la retrouver... avec pour succès le tirage dans A. On cherche donc la proba d'avoir x-1 succès au n-1 eme tirage ET que le nème soit un succès...

[tsinapah]

Ok je reformule l'énoncé :

n = nombre de boules total,
= nombre de boules dans l'urne ,
k = nombre d'urnes,

Trouver p(tirer la xième boule de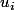 au tième tirage).

Non Hydre, je ne pense pas que P(tirer la première boule dans A) = na/n,
A chaque tirage, on a le choix entre les urnes qui restent donc si na>0 :
P(tirer la première boule dans A) = 1/

Le problème est de savoir entre combien d'urnes on a à choisir à chaque tirage, tout dépend de ce qui a déjà été tiré...

Il y a bien moyen de trouver la réponse en essayant toutes les combinaisons mais il y en a beaucoup ( ) et avec un grand nombre de boules et d'urnes, on risque de ne pas obtenir la reponse dans un temps raisonnable...

Je cherche donc une formule pour connaitre la probabilité de tirer la xième boule de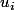 au tième tirage sans avoir à tester toutes les combinaisons... celà dépend, je pense, de la probabilité d'avoir tiré x-1 boules de 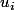apres t-1 tirages et de la probabilité de choisir l'urne au tième tirage (qui dépend du nombre d'urnes non vides restantes...).

Quelqu'un a une idée? Parce que moi j'ai beau retourner le problème dans tous les sens, je n'arrive pas à trouver une formule pour calculer çà...HELP!!!