Primitives successives

[Pseuda]

Bonjour,

J'ai une autre question qui me turlupine depuis un moment. J'ouvre un autre topic pour cela.

Quand on étudie une fonction, on s'intéresse à sa dérivée première, puis seconde, etc... . Pour une fonction, on s'intéresse à ses primitives. Pourquoi ne s'intéresse-t-on pas à ses primitives successives ? Oui bon, j'ai presque répondu à la question en la posant. Vos avis ?

[mathelot]

bonjour,
pour obtenir un DL des fonctions sinus et cosinus au voisinage de 0, on effectue des intégrations successives:
pour






etc...

[Ben314]

Salut,
Si, on s'y intéresse de temps en temps, mais en fait rarement sous le forme explicite de "primitive de primitive" vu que, si est un intervalle de et est continue, alors une primitive de est avec 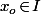et une "primitive de primitive", c'est .
Sauf que
Et je pense que, écrit sous cette forme là, ben ça ressemble plus à des trucs "qu'on étudie assez souvent"...

(et tu cherchera tout seul comment s'écrit une "primitive de primitive de primitive" à l'aide d'une seule intégrale)

[Skullkid]

Bonjour, quelques éléments de réponse pour faire avancer le schmilblick :

- L'intégration est une opération globale alors que la dérivation est une opération locale (on intègre sur un intervalle, on dérive en un point), du coup l'information contenue dans une intégrale est souvent plus compliquée à "faire parler".

- Prendre des primitives successives te donne des fonctions à un polynôme près, ce qui rajoute en quelque sorte des degrés de liberté superflus.

- En général, c'est plus facile de calculer une dérivée qu'une primitive (théorème de Liouville et compagnie).

[pascal16]

En mécanique, quand on part de la puissance fournie, il faut intégrer 2 fois pour retrouver la position.
Mais on ne va pas plus loin.
Idem avec des champs vectoriels et ED en mécanique des fluides

La primitive c'est aussi la moyenne, la surface, mais on ne va pas plus loin

Rectifier un arc -> seulement 1 primitive.


Mais, les moments d'ordre n sont bien une espèce de famille de primitives dont on augmente la complexité et qui ont une utilité en mécanique.

[Pseuda]

Bonjour et merci à tous pour vos réponses.

Mais curieusement, aucun de vos messages ne correspond à ce qui m'est venu en premier à l'esprit : les dérivées successives sont utiles pour étudier les fonctions et les courbes (sens de variation, convexité, point anguleux, etc ...). La succession des dérivées donnent des renseignements de plus en plus précis sur l'allure d'une courbe au voisinage d'un point (formule de Taylor), à tel point que si on en dispose suffisamment, on peut construire la courbe dans sa totalité (fonction DSE, à l'intérieur du rayon de convergence) ! (mais là, je ne suis pas trop sûre de moi).

Les primitives servent à calculer les aires (ou des moyennes, etc...). On peut les utiliser (exemple de Mathelot) pour obtenir des encadrements, mais cela se fait pas à pas, il n'y a pas de formule générale.

Par contre :

Salut,
Si, on s'y intéresse de temps en temps, mais en fait rarement sous le forme explicite de "primitive de primitive" vu que, si est un intervalle de et est continue, alors une primitive de est avec et une "primitive de primitive", c'est .
Sauf que
Et je pense que, écrit sous cette forme là, ben ça ressemble plus à des trucs "qu'on étudie assez souvent"..

Tu veux dire que les primitives successives se ramènent à l'intégration multiple, sur des variables différentes ? Dans ce cas en effet, on les étudie sans le dire.

[mathelot]

Sauf que

bonsoir Ben,
je n'ai pas compris cette égalité -j'ai vû qu'elle était vraie en calculant les deux membres
via et - mais je ne la comprends pas en terme d'intégrales doubles..

[Ben314]

En terme d'intégrale double, pour fixés (*) tu intègre sur le le demi carré que tu peut paramétrer soit en commençant par puis soit en commençant par puis (c'est le fameux théorème de Fubini)

(*) Si il faut inverser les intégrales et les inégalités, mais ça ne change pas le résultat.

Et sinon, des "primitives multiples", ça se ramène à une et une seule intégrale (à paramètre) et c'est en général plutôt comme ça qu'on manipule des "primitives multiples".

[mathelot]

Sauf que
Et je pense que, écrit sous cette forme là, ben ça ressemble plus à des trucs "qu'on étudie assez souvent"...

c'est le produit de convolution de avec f