Puissance successives de matrice
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nico2b
- Membre Relatif
- Messages: 271
- Enregistré le: 16 Jan 2007, 17:33
-
 par nico2b » 11 Juin 2007, 09:48
par nico2b » 11 Juin 2007, 09:48
Bonjour, il nous est demandé de déterminer les puissances successives de la matrice
A =
_{1\leq i,j \leq n})
=
)
(Matrice identité où la ligne diagonale est remonté)
Je ne comprends pas très bien la résolution donnée:
Soient 1

n , il vient
(A²
_{ij})
=

=
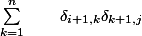
Jusque là ok il ne fait que remplacer... Mais enuiste il met l'égalité suivante :
=
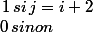
et je ne vois pas comment il a fait pour trouver ceci par rapport à la somme.
Quelqu'un pourrait-il m'expliquer?
Merci d'avance pour votre aide
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 11 Juin 2007, 09:57
par mehdi-128 » 11 Juin 2007, 09:57
Bonjour,en fait fais le produit matriciellement de toi meme et tu verra que la surdiagonale composée de 1 va remonter a chaque fois ,le reste il y aura que des 0.Ce qui donne le résultat voulu....
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 11 Juin 2007, 10:03
par mehdi-128 » 11 Juin 2007, 10:03
Par ailleurs pour mieux répondre a ta question,si je note s le produit de kronecker:
s(i+1,k)*s(k+1,j)= 1 si j=k+1+1=k+2
Car: s(i+1,k)=1 si k=i+1
s(k+1,j)=1 si j=k+1
On en déduit le résultat,la somme disparait il ne reste qu'un élément.....
-
nico2b
- Membre Relatif
- Messages: 271
- Enregistré le: 16 Jan 2007, 17:33
-
 par nico2b » 11 Juin 2007, 10:09
par nico2b » 11 Juin 2007, 10:09
Oui daccord mais cette relation 1 si j = i+2 et 0 sinon on peut la retrouver dnas les sommes?
Parce que ensuite pour A³, il trouve

et ensuite il faut en faire une preuve par récurrence pour vérifier pour

si c'est bien
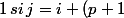 \\ 0 \, sinon)
.
Je me demandé si on ne pouvais pas se servir de la somme pour prouver ceci... Je sais pas si je me suis fait comprendre lol
Merci pour ton aide
-
nico2b
- Membre Relatif
- Messages: 271
- Enregistré le: 16 Jan 2007, 17:33
-
 par nico2b » 11 Juin 2007, 10:16
par nico2b » 11 Juin 2007, 10:16
mehdi-128 a écrit:Par ailleurs pour mieux répondre a ta question,si je note s le produit de kronecker:
s(i+1,k)*s(k+1,j)= 1 si j=k+1+1=k+2
Car: s(i+1,k)=1 si k=i+1
s(k+1,j)=1 si j=k+1
On en déduit le résultat,la somme disparait il ne reste qu'un élément.....
Ah oui ok je vois maintenant d'où viens le j = i+ 2 super merci :we:
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 11 Juin 2007, 10:31
par mehdi-128 » 11 Juin 2007, 10:31
de rien :).....
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
