Voici l'exercice que je ne comprends pas : Calculez le reste de la division :
Polynômes
4 messages
- Page 1 sur 1
Re: Polynômes
Je comprend pas trop : c'est le reste de la division de 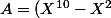(X^3-2X^2-X+2)) par quel polynôme
par quel polynôme  ?
?
Ou alors, c'est le reste de la division de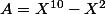 par
par 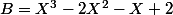 ?
?
Si c'est ça, tu part bien sûr de la formule générale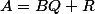 où, comme
où, comme \!<\!d^o(B)\!=\!3) on a
on a 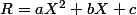 et ce qu'on cherche, c'est en fait les 3 réels
et ce qu'on cherche, c'est en fait les 3 réels  donc il faudrait 3 équations indépendantes.
donc il faudrait 3 équations indépendantes.
Ensuite, si on ne cherche que et pas
et pas  , il n'y a pas tellement le choix : il faut regarder ce que donne la relation
, il n'y a pas tellement le choix : il faut regarder ce que donne la relation =B(x)Q(x)+R(x)) lorsque
lorsque  est une racine de
est une racine de  (de façon à "tuer" le
(de façon à "tuer" le  dans la formule). Et si
dans la formule). Et si  admet des racines doubles (ou plus), ça signifie que
admet des racines doubles (ou plus), ça signifie que  annule non seulement
annule non seulement  mais aussi
mais aussi 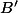 donc on dérive la relation
donc on dérive la relation 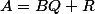 et on évalue en
et on évalue en  pour trouver une autre relation.
pour trouver une autre relation.
Comme admet 3 racines (compté avec ordre de multiplicité), ça donnera 3 relations -> Nickel.
admet 3 racines (compté avec ordre de multiplicité), ça donnera 3 relations -> Nickel.
Ou alors, c'est le reste de la division de
Si c'est ça, tu part bien sûr de la formule générale
Ensuite, si on ne cherche que
Comme
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Polynômes
Bonsoir, j'ai effectivement oublié de mettre le signe % entre les 2 parenthèse.
Je ne pense pas devoir utiliser la dérivée pour résoudre cet exercice. J'ai essayé de le résoudre en remplaçant par les racines de B dans la formule générale, comme vous l'avez expliqué. J'obtiens -1, 1 et 2 comme racines. J'obtiens alors 3 équations avec comme inconnues a, b et c. Mais lorsque je résous le système, mon reste vaut 510x^2-510.
Je ne pense pas devoir utiliser la dérivée pour résoudre cet exercice. J'ai essayé de le résoudre en remplaçant par les racines de B dans la formule générale, comme vous l'avez expliqué. J'obtiens -1, 1 et 2 comme racines. J'obtiens alors 3 équations avec comme inconnues a, b et c. Mais lorsque je résous le système, mon reste vaut 510x^2-510.
Re: Polynômes
Les 3 équation c'est :
x=2 => 4a + 2b + c = 1020
x=1 => a + b + c = 0
x=-1 => a - b + c = 0
et la solution, c'est a=340 ; b=0 ; c=-340
x=2 => 4a + 2b + c = 1020
x=1 => a + b + c = 0
x=-1 => a - b + c = 0
et la solution, c'est a=340 ; b=0 ; c=-340
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
