Polynômes

[doudours974]

Bonjour
Quelqu'un pourrait m'aider pour un exercice sur lequel je stagne ....

Soit f la fonction sur R(X) tel que f(P)=P(X+1)-P(X) pour tout polynôme P.

La première question était de montrer que f est linéaire.
Après j'ai déterminé l'ensemble Ker(f) des polynômes P tels que f(P)=0. J'ai trouvé l'ensemble des polynômes constants.

On définit ensuite une famille de polynômes (Jn) telle que Jn=1/n!*X*(X-1)*........*(X-n+1) avec Jn=1.
On nous demande de calculer f(Jn) en fonction de n. J'ai trouvé f(Jn)=Jn-1

Les questions suivantes sont :
- soit Q appartenant à R(X)un polynôme. Comment trouver P appartenant à R(X) tel que f(P)=Q ?
- Déterminer P pour Q = X^2 tel que P(1)=O.

Merci pour vos contributions.
-

[aviateur]

Bonjour
tu veux surement dire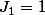
Je n'ai pas vérifié mais si on a bien = et comme forme une base de R[X]
alors si
on a
On obtient ainsi un antécédent de Q.

[doudours974]

Merci