Bjour, j'aurais besoin d'aide pour l'exo suivant:
Soit a1...an n entiers distincts
monter que le polynome (X-a1)(X-a2)..(X-an)-1 est irréductible dans Q
Polynome irréductible
7 messages
- Page 1 sur 1
L'irréductibilité peut se démontrer sur Z (puisque le polynôme est unitaire à coefs entiers).
Maintenant écrivons une factorisation du polynôme...(X-a_n)-1) en PQ où P et Q sont des polynômes unitaires à coeffs dans Z. Montrons alors que P ou Q est forcément constant (...et le résultat sera acquis).
en PQ où P et Q sont des polynômes unitaires à coeffs dans Z. Montrons alors que P ou Q est forcément constant (...et le résultat sera acquis).
Pour tout i, on a Q(a_i) = -1) . Mais nous travaillons sur Z, si bien que
. Mais nous travaillons sur Z, si bien que  = \pm 1 = - Q(a_i)) .
.
Ainsi le polynôme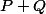 s'annule en
s'annule en 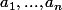 . Or
. Or 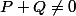 puisque P et Q sont unitaires. Donc
puisque P et Q sont unitaires. Donc  \geq n) . Ainsi
. Ainsi 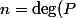+\deg(Q) \geq \max(\deg(P), \deg(Q)) \geq \deg(P+Q) \geq n)
ce qui force=0) ou
ou =0) .
.
Remarque : le résultat est faux avec...(X-a_n)+1) .
.
Maintenant écrivons une factorisation du polynôme
Pour tout i, on a
Ainsi le polynôme
ce qui force
Remarque : le résultat est faux avec
Si ton polynôme F est réductible sur Q, tu as F=PQ, avec P et Q à coefs rationnels. En multipliant par un entier n>0 convenable on obtient 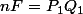 , avec
, avec  et
et 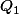 à coefs entiers. On peut supposer n minimal de sorte que les coefs de
à coefs entiers. On peut supposer n minimal de sorte que les coefs de  soient premiers entre eux et pareil pour
soient premiers entre eux et pareil pour 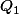 . Mais il y a un lemme de Gauss sur le "contenu" d'un polynôme (PGCD de ses coefs) qui dit que
. Mais il y a un lemme de Gauss sur le "contenu" d'un polynôme (PGCD de ses coefs) qui dit que =c(P_1)c(Q_1)) . D'où n=1 et donc P et Q sont à coefs entiers.
. D'où n=1 et donc P et Q sont à coefs entiers.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
