Polynôme irréductible
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 31 Jan 2010, 17:03
par Nightmare » 31 Jan 2010, 17:03
Salut !
Je viens de découvrir ce critère amusant :
Si p est un nombre premier, le polynôme
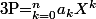
, avec
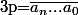
en base 10, est irréductible sur
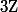
.
Ce critère se déduit-il du critère d'Eisenstein? Je n'en ai pas l'impression.
:happy3:
-
tito
- Membre Naturel
- Messages: 95
- Enregistré le: 13 Fév 2008, 14:21
-
 par tito » 31 Jan 2010, 17:46
par tito » 31 Jan 2010, 17:46
Bonjour Nightmare
Cette proposition semble fausse pour les nombres premiers entre inférieurs à 10
2X est par exemple réductible dans Z[X], aprés pour le cas supérieur à 10 il est clair que P est un polynôme primitif... il resterait à montrer qu'il est bien irréductible sur Q, ce qui ne semble pas évident...
amicalement
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 31 Jan 2010, 17:56
par ffpower » 31 Jan 2010, 17:56
Salut :we:
Tito: Si tu regardes le nombre 2, alors il correpond au polynome constant egal a 2, qui est bien irréductible..2X, ca correspond a 20..
Night: Ce résultat ( très amusant ) a déja été abordé sur le forum . Tu devrais trouver tout ce qu'il te faut ( et même plus^^) ici :
http://maths-forum.com/showthread.php?t=89102
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 31 Jan 2010, 19:04
par Nightmare » 31 Jan 2010, 19:04
Niquel ! Merci ffpower :happy3:
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 31 Jan 2010, 19:35
par Finrod » 31 Jan 2010, 19:35
tito a écrit:Bonjour Nightmare
Cette proposition semble fausse pour les nombres premiers entre inférieurs à 10
2X est par exemple réductible dans Z[X], aprés pour le cas supérieur à 10 il est clair que P est un polynôme primitif... il resterait à montrer qu'il est bien irréductible sur Q, ce qui ne semble pas évident...
amicalement
pour 2X le produit des coeff est nul, donc différent de 2, car le coef constant est nul.
Je ne sais pas si c'est ce que voulait dire ffpower.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
, avec
en base 10, est irréductible sur
.
, avec
en base 10, est irréductible sur
.