Petite question
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
par Babe » 03 Juin 2007, 17:16
bonjour
pour resourdre la solution homogene d'une equation differentielle du seconde ordre, je fais l'equation carac. et trouve delta=-3
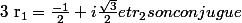
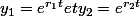
le prof arrive à
)
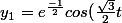et
)
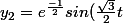comment passe t-il au cosinus et sinus ? (je me doute qu'il ya du e^ix=cos x +i sin x mais je ne trouve pas pareil )
merci d'avance
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
par allomomo » 03 Juin 2007, 17:29
Salut,
Si
et
,
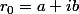
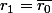
sont solutions de l'équation caractéristique.
Alors les solutions des l'équation homogène sont de la forme :
= e^{ax}\Big(C_1 \cos(bx)+C_2 sin(bx)\Big))
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
par Babe » 03 Juin 2007, 17:32
non mais en faite ma question c'est comment passe ton de
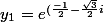t})
à
)
-
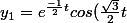allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
par allomomo » 03 Juin 2007, 17:40
Il faut trouver les constantes.
Tu n'oublie pas un 't' ?
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
par Babe » 03 Juin 2007, 17:59
ouai il y a un t, edit
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
par allomomo » 03 Juin 2007, 18:05
Si on prend
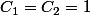
, on a ce que tu cherches.
Mais ces constantes dépendent des conditions initiales.
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
par Babe » 03 Juin 2007, 18:11
mon prof cherche y1 et y2 de cette maniere sans constante, car ce sont les base de l'espace vectorielle des solutions homogenes
mais apres dans la solution general il rajoute les constantes
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
