Petit exo marrant

par **Daniel-Jackson** » 01 Juin 2007, 20:35

Salut tout le monde , je ne sais pas si cet exo a été déjà proposé mais je me lance quand même.

Montrer que le groupe orthogonale O(n) est un groupe compact maximal de GLn(R)

Je le trouve marrant comme exo alors j'ai voulu vous le faire connaitre si ce n'est déjà fait.
Enjoy

par **Blueberry** » 01 Juin 2007, 21:00

Bonsoir, es-tu sûr de ce résultat ?

Si je prends les éléments de GLn(R) de norme comprise entre 1/2 et 2 au sens large. C'est un sous-groupe fermé et borné de GLn(R) donc compact et qui contient strictement On(R).

A moins que je ne fasse une erreur ?

par **yos** » 01 Juin 2007, 21:02

Salut.
Fermé comme image réciproque d'un singleton par

.
Borné car la norme euclidienne d'un élément est

.
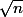
Donc compact car Mn(R) est de dimension finie.
Mais tu voulais peut-être parler du groupe topologique GLn(R) avec une topologie non héritée de l'evn Mn(R) ? J'y réfléchis, ainsi qu'à la maximalité.

par **Daniel-Jackson** » 01 Juin 2007, 21:05

yos a écrit:Salut.
Fermé comme image réciproque d'un singleton par .
Borné car la norme euclidienne d'un élément est .
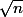
Donc compact car Mn(R) est de dimension finie.
Mais tu voulais peut-être parler du groupe topologique GLn(R) avec une topologie non héritée de l'evn Mn(R) ? J'y réfléchis, ainsi qu'à la maximalité.

Exactement je parle du groupe topologique GLn(R) . Et ma question revient à dire qu'il n'existe pas de sous groupe compact H de GLn(R) contenant strictement O(n) .

par **Daniel-Jackson** » 01 Juin 2007, 21:09

Blueberry a écrit:Bonsoir, es-tu sûr de ce résultat ?

Si je prends les éléments de GLn(R) de norme comprise entre 1/2 et 2 au sens large. C'est un sous-groupe fermé et borné de GLn(R) donc compact et qui contient strictement On(R).

A moins que je ne fasse une erreur ?

Es tu sûr que c'est un groupe multiplicatif ?

Tu prens A = 2I = B , AxB=4I n'est pas dans ce sous groupe .....

Sinon le résultat est certain !

par **Blueberry** » 01 Juin 2007, 21:13

Oui désolé j'aurai dû davantage réfléchir, ok.

par **Daniel-Jackson** » 01 Juin 2007, 21:22

Blueberry a écrit:Oui désolé j'aurai dû davantage réfléchir, ok.

No problem ça arrive :happy2:

par **Yipee** » 02 Juin 2007, 12:49

Il me semble (mais cela me parait trop simple) qu'il suffit de supposer que le sous-groupe K contient O(n) et une matrice M qui n'est pas dans O(n). On utilise alors la décomposition OS pour la matrice M et on en déduit qu'il existe une matrice symetrique définie positive (non égale à l'indentité car M n'est pas dans O(n)) donc une matrice diagonale. Il ne reste plus qu'a prendre ses puissances qui ne peuvent pas être bornée. Me trompe-je ?

par **yos** » 02 Juin 2007, 12:56

Il faut éventuellement prendre les puissances négatives de S.

par **Daniel-Jackson** » 02 Juin 2007, 14:30

Yipee a écrit:Il me semble (mais cela me parait trop simple) qu'il suffit de supposer que le sous-groupe K contient O(n) et une matrice M qui n'est pas dans O(n). On utilise alors la décomposition OS pour la matrice M et on en déduit qu'il existe une matrice symetrique définie positive (non égale à l'indentité car M n'est pas dans O(n)) donc une matrice diagonale. Il ne reste plus qu'a prendre ses puissances qui ne peuvent pas être bornée. Me trompe-je ?

Tu es sur la bonne voie !

par **Daniel-Jackson** » 02 Juin 2007, 14:31

yos a écrit:Il faut éventuellement prendre les puissances négatives de S.

Aussi oui !

Rste juste à rassembler tout ça et le tour est joué

Petit exo marrant

Petit exo marrant

Qui est en ligne