Petit CC (Base Orthonormale)

[Aispor]

Hello ! j'ai quelques question sur unE annale d'Algèbre en L2, le CC est demain ^^
je vous le laisse en entier dans ce post pour les curieux
Le voici :



J'ai plusieurs question que je vais mettre en plusieurs poste pour que ça soit plus lisible

Exercice 3:



Je suis resté à la question 5. Étant donné que l'on a jamais vu ça, et vu les questions précédente, je me doute que la réponse soit la matrice P : matrice de passage de la base canonique (1,x,x²,x(cube)) à la base orthonormale de W + W(orthogonal).
Mais bon ça serait le dire sans rien comprendre ^^"
Merci d'avance =)
M

[pascal16]

quand je vois le mot 'base' de la question précédente, j'aurais tendance à partir de la matrice de passage vers ou à partir de cette base

[Ben314]

Salut,
Déjà, pour ta culture, ça serait pas con d'éviter de confondre :
- DES Annales (nom féminin, normalement uniquement pluriel : UNE annale, ça se dit pas) : "Chronique qui rapporte les événements année par année".
- UN Annale qui n'existe pas, mais qui fait fortement penser à l'adjectif anal (qui peut bien sûr suivre un nom au masculin, comme dans "le stade anal") et dont la définition exacte est "qui fait référence à l'anus".
Bref, c'est quand même LA faute qui fait passer pour un . . . (qu'il vaut mieux éviter dans pas mal de circonstances)

Sinon, vu que tu as fait la question 1, ben c'est que tu sait ce que qu'est la matrice associée à une forme quadratique dans une base donnée.
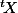
Et ça signifie que tu as forcément vu que, si S est la matrice (symétrique) de la forme bilinéaire dans la base B et si X est Y sont les vecteurs (colonne) des coordonnées de deux vecteurs x,y de E, alors (où est la transposé de X et en identifiant le résultat du calcul matriciel qui est une matrice 1x1 avec un scalaire).
Et maintenant, si tu as une autre base B', que la matrice de changement de base de B à B' est P alors les mêmes vecteurs x et y ont maintenant pour coordonnées (vecteurs colonne) X' et Y' tels que X=PX' et Y=PY' donc ce qui prouve que la matrice de de la forme bilinéaire dans la base B' est .
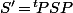
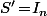
Ensuite, si B' est une base orthonormée (pour ), alors vu l'expression bien connu du produit scalaire dans une base orthonormée, on a en fait ce qui prouve que (si dim(E)=).
Et c'est évidement ces trucs là (que tu as forcément vu) qu'il faut que tu utilise.

[Aispor]

Ah oui je me demandais bien comment distinguer ces deux mots xD
Merci pour la réponse ^^

Enfin je comprend bien ! Merci beaucoup !

[vejitoblue]

Salut merci pour cet exo, j'essaye mais c hardcore pour moi.
Déjà je bloqué exo 2. Comment on trouve la dimension de F?

Édit bon je reviens de wiki. Mnn (K) serait de dimension nn, dont la base canonique est (Eij) I et j se baladant dans 1,n et Eij la matrice avec 1sur (i,j) et zéro ailleurs

F a bien l'air d'être de dimension 6 en prenant quelques éléments de la base canoniq
ue de Mnn, est ce qu'il ya une corrélation avec le nombre de zéro dans la matrice,je lignore ?

[Pseuda]

Bonsoir,

exo 2 : F est de dim 3. Il s'agit de décomposer M dans une famille libre de M3(R). Du coup, cette famille sera libre et génératrice de F, donc une base.

[vejitoblue]

Ok cimer
Concernant p(R) c'est la projection de R sur F? Donc que la trace de
tRM soit nulle avec M dans F? On se retrouve donc avec une matrice dont la diagonale est (0, 6b, -4b)?
p(R) c'est quoi? Ca devrait être une matrice?

[Pseuda]

Ok cimer
Concernant p(R) c'est la projection de R sur F? Donc que la trace de
tRM soit nulle avec M dans F? On se retrouve donc avec une matrice dont la diagonale est (0, 6b, -4b)?
p(R) c'est quoi? Ca devrait être une matrice?

Bonjour,

C'est la projection orthogonale de la matrice R sur le ss-e.v. F dont on vient de calculer une b.o.n. : c'est une matrice. Il suffit d'appliquer la formule du cours p(R)=(E1|R)E1+(E2|R)E2+(E3|R)E3, si (E1,E2,E3) est la b.o.n. trouvée à la question d'avant.

Par contre, la b.o.n. me paraît plutôt compliquée à trouver avec le procédé de Gram-Schmidt.

[Aispor]

Si tu veux je peux t'envoyer ce que j'ai fait :p

[Pseuda]

Si tu veux je peux t'envoyer ce que j'ai fait :p

Bonsoir,

Ok, ça m'intéresse.

[vejitoblue]

Coucou moi je veux bien voir ce que t'as fait.
Rassure moi pseuda Les matrices suivantes forment une base de F

[Pseuda]

Bonjour,

Oui, pourquoi as-tu besoin d'être rassuré ? C'est une famille libre (il suffit d'égaliser la matrice M=0 pour voir que tous les coefficients s'annulent), et génératrice de F (par définition de F).

[vejitoblue]

Nan j'avais vérifié mais des fois je crois dur comme fer à des trucs faux. J'ai encore du mal avec ces espaces.
Gram Schmidt désolé les cousins mais je suis trop fainéant, niksamer j'ai normé le premier vecteur de la base on se retrouve avec des racines de 7 et tout le Bataclan.
P(R) je l'ai normalement y a pas d'erreurs de calcul

Maintenant la distance... Ça a l'air facile quand on connaît les normes parce que sinon visuellement j'arrive pas à me représenter comment on "projette une matrice"

[Pseuda]

Comment as-tu fait pour avoir P(R) sans avoir la b.o.n. ? Je crois savoir mais bon. Une fois qu'on a P(R), la distance c'est RP(R).

[Ben314]

Ça a l'air facile quand on connaît les normes parce que sinon visuellement j'arrive pas à me représenter comment on "projette une matrice"

Là, vu la norme que tu as, c'est quand même sacrément crétin : ta matrice, au lieu de l'écrire "en 3x3", tu l'écrit "en 1x9" (ce qui, en terme d'espace vectoriel ne change absolument rien) donc tu est dans R^9 et en plus, la norme, ben c'est la norme Euclidienne usuelle sur R^9, donc tout ce qu'il y a de plus "visuel" (sauf éventuellement R^9 qui, je te l'accorde, dépassent "un peu" la perception visuelle standard humaine...)

Sinon, concernant l'orthogonalisation dans des cas comme celui là (i.e. purement calculatoire), c'est quand même un peu moins chiant (au niveau calculs) de commencer par tout orthogonaliser PUIS de normaliser (donc de ne pas appliquer l'algo. tel qu'on le trouve un peu partout "au pied de la lettre")

[Pseuda]

Bonsoir,

Concernant l'orthonormalisation des matrices de F, après une page de calculs assez pénibles, j'obtiens un résultat ... probablement faux. Donc, je me demande comment on peut donner cela en contrôle continu de 2h sans calculatrice.

j'ai normé le premier vecteur de la base on se retrouve avec des racines de 7 et tout le Bataclan.

Pour la 1ère matrice, j'ai trouvé 3 pour la norme.

Sinon, concernant l'orthogonalisation dans des cas comme celui là (i.e. purement calculatoire), c'est quand même un peu moins chiant (au niveau calculs) de commencer par tout orthogonaliser PUIS de normaliser (donc de ne pas appliquer l'algo. tel qu'on le trouve un peu partout "au pied de la lettre")

Mais avec le procédé de Gram-Schmidt, il faut normer les vecteurs au fur et à mesure, pour obtenir une base ne serait-ce qu'orthogonale ?

[Ben314]

Mais avec le procédé de Gram-Schmidt, il faut normer les vecteurs au fur et à mesure, pour obtenir une base ne serait-ce qu'orthogonale ?

Tout dépend bien évidement de comment tu procède :
- Si tu orthonormalise au fur et à mesure, alors si à déjà donné (orthonormée), alors pour redresser le vecteur suivant de la famille de départ, tu va calculer les (), puis et tu calcule au final .
- Si tu orthogonalise uniquement, alors si à donné (orthogonale uniquement), alors pour redresser , tu calcule les , puis .
Et à la fin, une fois (orthogonale) calculé. tu divisera les vecteurs par leur norme pour avoir

C'est clairement parfaitement totalement exactement tout à fait la même chose, sauf que
- Dans un cours, c'est plus joli les formules en bleu (plus concis...)
- Dans un exercice avec des "vrai vecteurs" (à coordonnées rationnelles...) et des calculs à faire à la main, ben la formule rouge et mieux vu qu'il n'y a pas de racine carrée à calculer nulle part donc les seront tous à coordonnées rationnelles.

Et soit dit en passant, c'est la même chose dans à peu près tout ce qui concerne l'orthogonalité, par exemple les projection orthogonales sur les s.e.v. et tout les trucs de ce genre là : en cours tu le fait avec des bases orthonormées, mais dans les "cas concret" (vecteurs connus et "vrai calculs" à faire), tu le fait toujours avec des bases orthogonales.

[Pseuda]

- Si tu orthogonalise uniquement, alors si à donné (orthogonale uniquement), alors pour redresser , tu calcule les , puis .
Et à la fin, une fois (orthogonale) calculé. tu divisera les vecteurs par leur norme pour avoir

Comment as-tu obtenu la base orthogonale ? C'est là où ça coince.

La formule ne marche qu'avec les vecteurs normés pour obtenir orthogonale au reste de la famille, donc il faut normer les vecteurs au fur et à mesure, non ?

EDIT : A moins que tu veuilles dire qu'on fait : .
Là ça marche, on obtient des vecteurs orthogonaux. Mais je viens de tester sur un exemple, le procédé est aussi long que de normer les vecteurs au fur et à mesure (autant de produits scalaires et de normes à calculer, mais pas de radicaux, je te l'accorde, mais vu qu'il faut ensuite normer les vecteurs, bof, cela revient au même).

[Aispor]

Finalement je me rend compte que je n'ai pas fait les calculs xD car Gram-Schimdt on l'a fait mille fois en TD.

Mais il est vrai que orthogonaliser une base de matrice (ce qu'on a eu cette année au CC, ça devient tout de suite TREEEEES long, avec des matrices a coefficient proche du millier qu'il faut mettre au carré xD.

Enfin l'enfer, et je comprend toujours pas pourquoi on nous demande ça au partiel car bon on passe une demi-heure sur un calcul qui se fait sur calculatrice aujourd'hui x).

D’ailleurs si tu veux vérifier ton résultat pseuda, ce que l'on fait nous c'est soit calculatrice (interdit a l'exam), soit tu regarde la dernière matrice que tu as calculer, et tu en fait le produit scalaire avec la première, qui est certainement juste, si ça donne 0 (les matrices sont orthogonales) il y a déjà pas mal de chance que tu as réussis

[Pseuda]

Merci, mais je ne vois pas comment automatiser ce calcul sur Wolfram, et encore moins sur calculatrice. Il faut tout lui cracher : transposition, produit, trace, ..., avec un risque d'erreur aussi important.

En contrôle continu, je pense qu'il faut passer cette question (1/2h sur 2h tout de même), mais le problème, c'est qu'on a en besoin pour la suite...