fatal_error a écrit:Mais tu pourrais aussi prendre un autre produit scalaire, par exemple
S=(0,1;-1,0)
Salut, attention c'est pas un produit scalaire cette matrice-là, il faut une matrice symétrique définie positive.
@Cryptocatron-11 : le calcul présenté par fatal_error c'est
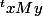
où x et y sont exprimés en colonne suivant une base donnée, et M est la matrice qui définit ton produit scalaire suivant cette base (jusqu'à présent vous avez choisi la base canonique de R² comme base de référence). Quand on fait le calcul avec ton exemple ça fait 21, fatal_error a fait une coquille.
Sinon je ne comprends pas ton premier post :
Cryptocatron-11 a écrit:ExempleSoit une base
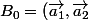)
avec
_B_0)
et
_B_0)
alors la base
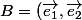)
est orthonormale , c'est bien ça ?
Si je comprends bien tes notations, e1 = a1 et e2 = a2 donc B = B0. Donc B est orthonormée si et seulement si B0 l'est.
Lorsque ton espace est muni d'un produit scalaire, une base orthonormée c'est une base
)
dont les vecteurs vérifient que
)
est égal à 1 si i = j et est égal à 0 sinon.
Par exemple, si on prend le produit scalaire usuel sur R², la base ((1,0),(1,1)) n'est pas orthonormée (les vecteurs sont exprimés dans la base canonique).
