Salut,
Je saisi pas trop l'exercice, en particulier d'où pourrait bien sortir le fait qu'il n'y a qu'un nombre fini d'orbite.
Si on prend l'application de N->N telle que 2n->2n+1 et 2n+1->2n, c'est clairement une permutation de E=N et il y a tout aussi clairement une infinité d'orbite, à savoir les {2n,2n+1}
Sinon, modulo d'appeler
_{i\in I})
les orbites, c'est correct (*) (mais I peut parfaitement être infini, voire tout ce qu'il y a de plus non dénombrable, par exemple si la permutation, c'est l'identité de R dans R).
Sinon, je comprend absolument pas ce que tu veut "démontrer" (surtout par récurrence) dans le 1. : pour démontrer les différent trucs (1. 2. et 3.), va évidement falloir qu'à un moment ou un autre tu
définisse qui sont les
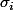
dont tu parle et il me semble très clairement que le 1. ben c'est ça que tu va prendre comme définition (des
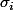
) ce qui fait que tu as que dalle à démontrer (à part que la définition est cohérente, c'est à dire que la restriction de

à
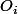
est bien une permutation de
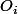
)
(*) Sauf que tu risque pas de parler "direct" du produit des
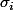
vu qu'à priori, c'est un produit infini (éventuellement non dénombrable) et que sans topologie, ça a a priori aucun sens.
Là, ça a du sens vu que quelque soit x, un et un seul élément du produit ne laisse pas x fixe donc on peut définire ce qu'est "le produit appliqué à x"
