Bonjour,
La question est si le sous-groupe de S6, engendré par l'ensemble des deux permutations: (12)(34)(56) et (145)(236) est cyclique ou pas, puis même question pour (123), (456).
Merci de m'aider à comprendre.
Sous-groupe engendré par des permutations
6 messages
- Page 1 sur 1
Re: sous-groupe engendré par des permutations
Si un groupe est engendré par deux éléments a et b, alors l'ordre du groupe doit être un multiple commun des ordres de a et de b. Ça donne peut donner une idée pour le premier groupe.
Le deuxième groupe est facile à décrire.
Le deuxième groupe est facile à décrire.
Re: sous-groupe engendré par des permutations
Bonjour,
donc le premier sous-groupe est d'ordre 6 car c'est le plus petit sous-groupe de S6 qui contient les deux permutations données et alors c'est {e, (12)(34)(56),(145)(236),(135246),(642531),(632)(541)}, il est cyclique car il possède deux éléments d'ordre 6.
pour le second sous-groupe j'ai trouvé qu'il est composé de 9 éléments, et qu'il ne possède aucun élément d'ordre 9, donc non cyclique.
Prière de me dire si ma réponse est correcte. Merci d'avance.
donc le premier sous-groupe est d'ordre 6 car c'est le plus petit sous-groupe de S6 qui contient les deux permutations données et alors c'est {e, (12)(34)(56),(145)(236),(135246),(642531),(632)(541)}, il est cyclique car il possède deux éléments d'ordre 6.
pour le second sous-groupe j'ai trouvé qu'il est composé de 9 éléments, et qu'il ne possède aucun élément d'ordre 9, donc non cyclique.
Prière de me dire si ma réponse est correcte. Merci d'avance.
Re: sous-groupe engendré par des permutations
Oui c'est ça. Le premier sous-groupe est isomorphe à 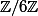 , le deuxième à
, le deuxième à 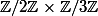 .
.
Re: sous-groupe engendré par des permutations
Vous voulez dire pour le deuxième, Z/3Z x Z/3Z.
Merci beaucoup pour votre assistance.
Merci beaucoup pour votre assistance.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
