Periode du courbe paramétrée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 28 Fév 2007, 00:25
par MacErmite » 28 Fév 2007, 00:25
Bonjour,
J'ai un petit problème avec cette fonction:
=cos(\frac{3\theta}{2}) +\frac{\sqrt{2}}{2})
Sa représentation graphique (polaire) me pose un soucis. Je pensais jusqu'à présent qu'il suffisait de prendre

dans l'interval de la prériode pour dessiner entièrement cette courbe. Mais il n'en est rien, en effet si je trace de
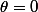
jusqu'à
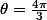
le graph est incomplet ! (merci la calculatrice). Mais je ne comprends pas pourquoi elle reste incomplette alors que j'ai varié l'angle polaire sur une période ?
(j'avais posé cette question par erreur dans "lycée" mais je ne sais pas comment revenir en arrière)
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 28 Fév 2007, 01:25
par abcd22 » 28 Fév 2007, 01:25
Bonsoir,
C´est parce que pour que 2 points
))
et
))
d´une courbe en polaires coincident il faut soit

et
 = \rho(\theta))
, soit

et
 = - \rho(\theta))
, dans la définition de ta période tu as tenu compte seulement de la coordonnée rayon et pas de l´angle, ici la période est
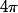
. Comme
 = \rho(\theta))
, on peut réduire l´intervalle d´étude à
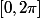
et déduire la 2e moitié de la courbe par symétrie par rapport à l´axe des abscisses.
-
mathelot
 par mathelot » 28 Fév 2007, 11:11
par mathelot » 28 Fév 2007, 11:11
Bonjour,
La mesure

de l'angle polaire est un réel variant de

à

.
En partant d'une mesure égale à

, on cherche

tel que la courbe se "referme" pour la première fois. On cherche donc
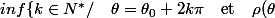= \rho(\theta_{0}) \})
et
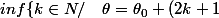 \pi \quad \mathrm{et} \quad \rho(\theta)= - \rho(\theta_{0}) \})
et ensuite, le plus petit de ces deux inf.
Dans l'exemple que tu as choisi, il y a bien eu un balayage de
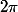
,
mais ça n'a pas suffit à "refermer" la courbe, c'est à dire à paramétrer un lacet.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
