Courbe paramétrée et point multiple

[Noub]

Bonjour,
Je cherche à démontrer l'unicité d'un point multiple de la courbe paramétrée par
x(t)=t-t^3
y(t)=t^2-t^4
Après l'étude de la courbe, je sais que c'est 0, mais la démonstration c'est autre chose.
Et ensuite de déterminer une équation cartésienne de cette courbe
Merci

[LN1]

Bonjour,

Le plus simple ici est de rechercher une relation simple entre x et y




tu cherches à trouver t et a tels que
M(t) = M(a) avec a différent de t

cela se traduit par



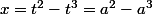
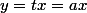
puisque t et a sont différents, la seconde égalité implique que x = 0
donc que y = 0

Le seul point multiple ne peut être que O

Vérification : O est un point multiple car O = M(0)=M(1) =M(-1)

Pour trouver une équation cartésienne de (C), il te faut éliminer t
*Pour x non nul, c'est facile

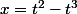
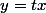donc
il te suffit de remplacer dans la première équation, de multiplier par pour faire plus joli

* pour x = 0
il te suffit de vérifier que l'équation que tu as obtenue pour x différent de 0 "marche" aussi pour x = 0