Pblm de probabilité

[cdm1024]

Bonjour,

Voici un problème de probabilité et ma réponse. Est-ce correct, et comment on aurait pu faire?


Au poker, une main et un ensemble de 5 cartes extraites d'un jeu de 32 cartes.

On rapelle que:

- les hauteurs sont: 7,8,9,10,V,D,R,A
- les couleurs sont: T,CA,CO,P

1- Combien il y a de mains possibles.

Une main est équivalent aux tirages successifs sans remise de 5 cartes de 32. Donc il y a 32*31*30*29*28 mains

2- Quelle est la probabilité d'obtenir chacune des mains suivantes:

2.1- un quinte (cinq cartes de hauteurs consécutives, et de même couleur):

Si on tire un 7: il reste à tirer (8,9,10,V). Donc P(7)=1/32*1/7*1/6*1/5*1/4
Si on tire un 8: il reste à tirer (7,9,10,) ou (9,10,V,D). Donc p(8)=1/32*1/7*1/6*1/5*1/4+1/32*1/7*1/6*1/5*1/4
Si on tire un 9: il reste à tirer (7,8,10,V) ou (8,10,V,D) ou (10,V,D,R). Donc p(9)3*(1/32*1/7*1/6*1/5*1/4)
Si on tire un 10: il reste à tirer (7,8,9,V) ou (8,9,V,D) ou (9,V,D,R) ou (V,D,R,A). Donc P(10)=4*(1/32*1/7*1/6*1/5*1/4)
Si on tire un V: il reste à tirer (7,8,9,10) ou (8,9,10,D) ou (9,10,D,R) ou (10,D,R,A). Donc P(10)=4*(1/32*1/7*1/6*1/5*1/4)
Si on tire un D: il reste à tirer (8,9,10,V) ou (9,10,V,R) ou (10,V,R,A). Donc P(10)=3*(1/32*1/7*1/6*1/5*1/4)
Si on tire un R: il reste à tirer (9,10,V,D) ou (10,V,D,A). Donc P(10)=2*(1/32*1/7*1/6*1/5*1/4)
Si on tire un A: il reste à tirer (10,V,D,R). Donc P(10)=(1/32*1/7*1/6*1/5*1/4)
Donc la propabilité de tirer un quinte est P=(1+2+3+4+4+3+2+1)*(1/32*1/7*1/6*1/5*1/4)

Merci d'avance de vos réponses.

[cdm1024]

Apparement mon problème n'intéresse personne.

Je corrige ma réponse à la première réponse. c'est une réponse plus juste.

J'aimerai juste savoir si mon raisonnement est bon.

Merci

[nuage]

Salut,
En effet me semble une bonne réponse à la question 1 (l'ordre d'arrivée des cartes n'a pas d'importance)
Pour les quintes : si on range les cartes dans l'ordre croissant il est faciles de voir que la quinte commence par 7, 8, 9 ou 10.
Si on veut que toutes les cartes soient de la même couleur on a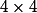 choix possibles. Soit une proba de ce qui est assez différent de ce que tu as trouvé.
Si on ne le demande pas ton raisonnement est faux car la proba de tirer (7,8,9,10,V) dans cet ordre est avec des erreurs du même genre pour les autres cas.

Ce type de raisonnement,tenant compte de l'ordre, me semble possible, mais très compliqué.

Il me semble plus simple de se poser la question combien y a t-il de quintes (7,8,9,10,V) sans tenir compte de l'ordre? (il suffit de choisir les couleurs).
Puis multiplier ce résultat par 4 (hauteurs possibles) et diviser le tout par pour avoir la probabilité.

Apparement mon problème n'intéresse personne.

[CENTER]:zen: il ne faut pas être trop impatient :zen:[/CENTER]