Sn++ ouvert de Sn

[acteon]

Bonjour,
je voudrais montrer que Sn++(R) est un ouvert de Sn(R).
c'est assez facile de montrer que Sn++(R) est un ouvert de Sn+(R) (par exemple car Sn++ est l'ensemble des matrices de Sn+ de déterminant non nul) mais pour Sn++ dans Sn, c'est un peu plus délicat. Si on bouge dans une petite boule autour d'une matrice de Sn++, tout en restant dans Sn, (si B=A+C avec C symétrique de petite norme) les valeurs propres ne vont pas beaucoup bouger. mais comment en dire plus? on ne peut pas codiagonaliser. Par les polynômes caractéristiques ?
Merci à qui pourra m'aider!

[GaBuZoMeu]

Bonjour,
Que veux-tu dire par "on ne peut pas codiagonaliser ? Que dit le théorème spectral quand on a ?deux formes quadratiques dont l'une est définie positive ?
Sinon, on peut utiliser le fait qu'une forme quadratique
est définie positive si et seulement si son minimum sur la sphère unité (qui est compacte) est strictement positif.

[acteon]

En fait je voudrais rester dans le cadre du programme de prépa, donc sans forme quadratique...j'aurais du le préciser pardon

[GaBuZoMeu]

Forme quadratique ou matrice symétrique, c'est kif-kif.
La forme quadratique associée à une matrice symétrique , c'est simplement .

[acteon]

Ok merci je pensais que tu proposais d'utiliser théorème de diagonalisation simultanée etc...
donc , Sn++ est l'image réciproque de R+* par la fonction f qui à S dans Sn associe le min de XTSX sur la boule unité. Ok on sait que XTSX prend toutes les valeurs entre kmin et kmax (valeurs propres). Cette fonction est un peu compliquée, est il aisé de prouver sa continuité?
Merci en tout cas et bonne journée

[GaBuZoMeu]

On peut montrer le résultat général suivant :
Soit un espace métrique, un espace métrique compact, une fonction continue. On définit par . C'est bien défini puisque, pour tout , la fonction continue est bornée et atteint ses bornes sur le compact .
Alors est continue. Je te laisse faire la démonstration. On prend une suite d'éléments de qui tend vers et il faut montrer que pour tout 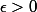, on a et à partir d'un certain rang.
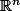Ce résultat s'applique pour l'espace des matrices symétriques réelles de taille , la sphère unité dans et .

[acteon]

Je te remercie je vais regarder ça