Bonsoir,
j'ai un léger trou, j'espère que vous pourrez m'éclaircir.
Lorsqu'on a une fonction a plusieurs variables f(x,y) ici pour simplifier le problème.
Si je dérive la fonction par rapport à x j'ai comme notation.
df/dx
Mais maintenant, là où j'ai mon petit 'trou'
Si je dérive de nouveau cette dérivé par rapport à y cette fois
j'ai
d2f/dxdy
ou bien
d2f/dydx
C'est juste une question de notation dont je ne suis plus sûr...problématique quand on doit calculer des matrices hessienne =)
Merci pour votre réponse^^
Notation de dérivée
5 messages
- Page 1 sur 1
Notation de dérivée
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
Re: Notation de dérivée
Salut,
Bon, ben ça part pas gagné.....
Le mini du mini du mini à savoir quand on utilise même à peine des dérivées partielles d'ordre 2 (ou plus), c'est le théorème de Schwarz qui te dit que, si f est C^2, alors d/dy(df/dx)=d/dx(df/dy) (donc que, la matrice Hessienne est symétrique donc R-diagonalisable dans une base orthonormée)
Et a mon avis, pour un matheux, ça fait aussi parti du "bagage minimum" de connaitre un contre exemple (où bien entendu f n'est pas C^2).
Sinon, ben de façon vachement surprenante,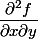 , c'est une abréviation de
, c'est une abréviation de )
et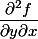 , c'est une abréviation de
, c'est une abréviation de ) .
.
Bon, ben ça part pas gagné.....
Le mini du mini du mini à savoir quand on utilise même à peine des dérivées partielles d'ordre 2 (ou plus), c'est le théorème de Schwarz qui te dit que, si f est C^2, alors d/dy(df/dx)=d/dx(df/dy) (donc que, la matrice Hessienne est symétrique donc R-diagonalisable dans une base orthonormée)
Et a mon avis, pour un matheux, ça fait aussi parti du "bagage minimum" de connaitre un contre exemple (où bien entendu f n'est pas C^2).
Sinon, ben de façon vachement surprenante,
et
Modifié en dernier par Ben314 le 11 Déc 2016, 18:59, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Notation de dérivée
Salut !
C'est la deuxième forme (d'ailleurs, je ne sait pas si tu as eu la flemme de l'écrire, mais ce ne sont pas des " " mais plutôt des "
" mais plutôt des " ") :
") :
 \right) = \dfrac{ \partial^2 f}{ \partial y \partial x } (x,y))
C'est la deuxième forme (d'ailleurs, je ne sait pas si tu as eu la flemme de l'écrire, mais ce ne sont pas des "
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Notation de dérivée
Bonjour,
il me semble que l'on commence par df/dx puis d[df/dx]/dy, ce qui s'écrit d²f/(dydx)
Edit : Bon, pas très rapide et pas joliment écrit.
il me semble que l'on commence par df/dx puis d[df/dx]/dy, ce qui s'écrit d²f/(dydx)
Edit : Bon, pas très rapide et pas joliment écrit.

Re: Notation de dérivée
Si ça peut vous rassurer je suis plus informatique que matheux :p
Donc si je résume
Si on dérive d'abord par x, ensuite par y on note ça: d[df/dx]/dy<=> d²f/(dydx)
Si on dérive d'abord par y, ensuite par x on note ça: d[df/dy]/dx<=> d²f/(dxdy)
Pour l'écriture du d, oui pas de soucis, disons juste que même sur papier j'ai tendance à faire un d un peu courbé donc =) Mais oui on est d'accord pour la notation ce n'est pas un d^^
Merci de vos réponses
Donc si je résume
Si on dérive d'abord par x, ensuite par y on note ça: d[df/dx]/dy<=> d²f/(dydx)
Si on dérive d'abord par y, ensuite par x on note ça: d[df/dy]/dx<=> d²f/(dxdy)
Pour l'écriture du d, oui pas de soucis, disons juste que même sur papier j'ai tendance à faire un d un peu courbé donc =) Mais oui on est d'accord pour la notation ce n'est pas un d^^
Merci de vos réponses
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
