Non-continuité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 05 Jan 2008, 11:47
par fenecman » 05 Jan 2008, 11:47
Bonjour, je suis confronté à l'exercice suivant:
Le décor :
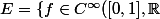 | \forall n \in \mathbb{N} , f^{(n)}(0)=0})
(On munit E de la norme de la convergence uniforme).
On pose
 | \forall x \in [0,1] ,\Phi(f)(x) = \int_0^{x} f(t) dt)
Et il faut que je montre que
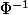
n'est pas continue, en utilisant la fonction f de E telle que
 = e^{-1/x^2}~~ et ~~ f(0)=0)
J'ai montré que
}(x)= \frac{P_n(x)}{x^{3n}} exp{-1/x^2})
.Je pensais montrer que
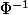
n'est pas borné sur la boule unité, enfin plutôt
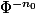
.
Est-ce que la démarche est valable?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 05 Jan 2008, 12:05
par tize » 05 Jan 2008, 12:05
Si
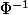
est continue alors il existe une constante
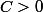
telle que :
}\)||_\infty\geq C.||f^{(n)}||_\infty)
i.e.
}||_\infty\geq C.||f^{(n)}||_\infty)
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 05 Jan 2008, 12:20
par fenecman » 05 Jan 2008, 12:20
Si
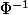
est continue alors il existe k>0 tel que
}\)\)||_\infty \le k.||\Phi(f^{(n)}\)||_\infty)
Donc je suis d'accord, mais je ne vois pas comment l'utiliser ...
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Jan 2008, 14:11
par ThSQ » 05 Jan 2008, 14:11
Y'a pas une relation de réc sur les Pn qui montrent que sup (P(n+1)/x^{n+1} / P(n)/x^{n}) -> +oo ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 05 Jan 2008, 14:33
par tize » 05 Jan 2008, 14:33
ThSQ a écrit:Y'a pas une relation de réc sur les Pn qui montrent que sup (P(n+1)/x^{n+1} / P(n)/x^{n}) -> +oo ?
J'ai essayé cela, j'ai trouvé un truc du genre :
=(2-3nx^2).P_n+x^3.P_n^'(x))
...mais franchement c'est pas génial...pourquoi, Fenecman, n'utilises tu pas plutôt un truc simple comme
=x^n)
...ça roule tout seul me semble-t-il...
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 05 Jan 2008, 15:53
par fenecman » 05 Jan 2008, 15:53
tize a écrit:pourquoi, Fenecman, n'utilises tu pas plutôt un truc simple comme
=x^n)
...ça roule tout seul me semble-t-il...
Mais g_n n'apparient pas à E , la derivé nème en 0 n'est pas nul, mais vaut n! ...
(Pour la relation entre les polynomes j'ai la même chose et j'en pense la même chose !!...)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 05 Jan 2008, 16:25
par tize » 05 Jan 2008, 16:25
Ah oui...c'est bête j'ai oublié cette condition...
Sinon on doit avoir :
}{x^{3(n-1)}} exp{-1/x^2}||_\infty\geq C.||\frac{P_n(x)}{x^{3n}} exp{-1/x^2}||_\infty)
si le sup de gauche est atteint en
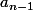
alors :
}{a_{n-1}^{3(n-1)}} \geq C.\frac{P_n(a_{n-1})}{a_{n-1}^{3n}})
et donc :
}{P_{n-1}(a_{n-1})a_{n-1}^3}=\frac{P_{n-1}^'(a_{n-1})}{P_{n-1}(a_{n-1})}+\frac{2-3na_{n-1}^2}{a_{n-1}^3})
d'après la relation de récurrence sur les polynômes.
Peut être que cela donne quelque chose comme l'idée de ThSQ....Je n'ai pas le temps de pousser plus loin, je dois y aller...à plus tard...
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 05 Jan 2008, 17:24
par fenecman » 05 Jan 2008, 17:24
Je craqqqqquuuueeee :mur: .
Esperons que demain ça aille mieux :marteau:
-
ju1s
- Membre Naturel
- Messages: 98
- Enregistré le: 02 Jan 2008, 15:02
-
 par ju1s » 05 Jan 2008, 17:29
par ju1s » 05 Jan 2008, 17:29
bonjour je ne compren rien lol a sque vous raconter mais je pense que vous avez le niveau pour repondre a un de mes sujet "formule général non comprise" c'est dans le collège mais personne ne peu m'aider si vous pouviez allez faire un tour et essayé de m'expliqué ce seré vrémen cool :happy2:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Jan 2008, 18:20
par ThSQ » 05 Jan 2008, 18:20
ju1s a écrit:bonjour je ne compren rien lol a sque vous raconter mais je pense que vous avez le niveau pour repondre a un de mes sujet "formule général non comprise" c'est dans le collège mais personne ne peu m'aider si vous pouviez allez faire un tour et essayé de m'expliqué ce seré vrémen cool :happy2:
mékikidi ?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 05 Jan 2008, 18:30
par ThSQ » 05 Jan 2008, 18:30
Je crois qu'on peut écrire :
}(x) = P_n(\frac{1}{x}) f(x))
avec

un polynome à coefficients
entiers et d°

= 13°, hipps, ou 3n c'est à voir et de coefficient dominant

On a donc
}(x)/f^{(n)}(x))
qui évolue au moins en
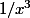
au voisinage de 0.
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 05 Jan 2008, 22:19
par Babe » 05 Jan 2008, 22:19
ju1s a écrit:bonjour je ne compren rien lol a sque vous raconter mais je pense que vous avez le niveau pour repondre a un de mes sujet "formule général non comprise" c'est dans le collège mais personne ne peu m'aider si vous pouviez allez faire un tour et essayé de m'expliqué ce seré vrémen cool :happy2:
oui c'est possible (enfin pas fenecman :ptdr: , vive les nuages )
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 06 Jan 2008, 09:22
par fenecman » 06 Jan 2008, 09:22
Babe a écrit:oui c'est possible (enfin pas fenecman :ptdr: , vive les nuages )
:we:
Babe le chimiste voudrait-il m'aider? !!! :zen:
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 06 Jan 2008, 13:01
par fenecman » 06 Jan 2008, 13:01
ThSQ a écrit:On a donc
}(x)/f^{(n)}(x))
qui évolue au moins en
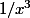
au voisinage de 0.
ça serait donc au voisinage de 0 qu'on trouve la contradiction?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 06 Jan 2008, 14:17
par ThSQ » 06 Jan 2008, 14:17
Clairement.
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 06 Jan 2008, 17:38
par fenecman » 06 Jan 2008, 17:38
Par contre ya un passage que j'ai pas bien compris :
ThSQ a écrit: d°

= 13°, hipps, ou 3n c'est à voir et de coefficient dominant

C bien écrit de degré 13 ??
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 07 Jan 2008, 20:30
par fenecman » 07 Jan 2008, 20:30
Si je pouvais juste avoir la précision sur le degré après promis j'arrete de vous embeter avec mon exercice !!
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 07 Jan 2008, 20:33
par ThSQ » 07 Jan 2008, 20:33
fenecman a écrit:Si je pouvais juste avoir la précision sur le degré après promis j'arrete de vous embeter avec mon exercice !!
Xcuze c'était un blague assez pitoyable (due à des abus de CH3-CH2-OH) le coup du 13°
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 07 Jan 2008, 21:20
par fenecman » 07 Jan 2008, 21:20
Merci !!
C'est moi qui avait l'esprit pas assez ouvert !!! J'aurais du le lire à haute voix ^^
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 07 Jan 2008, 22:06
par Babe » 07 Jan 2008, 22:06
abus de chimie= dangereux pour la santé
fenecman voila pourquoi tu a les poumons percés , un souffle au coeur ... :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités