Moyenne du Laplacien/Laplacien de la moyenne

[adrien69]

Salut tout le monde,
Je suis en train de me griller les neurones sur une étape d'un problème que je n'arrive tout bonnement pas à résoudre. C'est peut-être un point de calcul bidon mais je bloque.

Voilà donc le soucis :

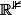
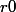
On note où tout se passe dans et où l'on considère , vous pouvez avoir les hypothèses de régularité que vous souhaitez sur u, ça importe peu.

Il faut alors montrer que .

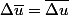
Et là le calcul me bloque.

Je vois très bien le sens physique, puisque le Laplacien mesure l'écart entre un point et la moyenne des points à son voisinage (d'où le sens de la propriété de la moyenne pour les fonctions harmoniques d'ailleurs), mais vraiment, le calcul explicite me bloque.

[Ben314]

Salut,
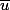
Bon, c'est pas du tout mon domaine (le laplacien par exemple... :hein:), mais ta fonction , ça serait pas la dérivée de l'intégrale triple sur le boule de rayon r de la même chose ?
Si c'est le cas, en écrivant l'intégrale triple sur la boule sous la forme d'une intégrale pour t de 0 à 1 de u(rt.y) où y décrit la sphère unité tu doit pouvoir dériver façilement le schmilblick autant de fois que tu veut il me semble.

P.S. en fait, ça sert pas à grand chose de passer à l'intégrale triple sur la boule : tu peut directement poser y=r.x dans ton intégrale de façon à ce que x décrive la sphère unité (et ça te vire agréablement la division par r² du départ, ce qui est pratique pour dériver...) :

et tu dérive 2 fois...

[adrien69]

Je suis on ne peut plus d'accord, mais quand tu intègres le laplacien ça se passe autrement plus mal...

[adrien69]

Oh mais je suis con !!!! Mea culpa, mea maxima culpa ! Un élément de volume en sphérique c'est !!!

Donc après, comme il faut utiliser l'expression du laplacien en sphérique, ça devrait assez bien se passer !

[adrien69]

En fait je n'ai même pas besoin de ça !


Fini.

J'aurais dû partir par là dès le départ. Merci pour le déblocage.
Par contre le calcul explicite me bloque toujours