Bonjour,
Je suis étudiant en d'école d'ingé. Pour mon projet de fin d'étude j'ai à réaliser un projet relatif à la mécanique dynamique des matériaux polymères... Je m'arrete ici pour les explications qui ne vous intéressent pas :ptdr:
Disons concretement que je suis face à un problème qui me semble assez complexe à résoudre. Pour le bien de mon projet je dois arriver à fitter une série de datas expérimentales avec une loi de comportement. Habituelllement, quand les lois de comportement sont plus ou moins linéaires (où tout du moins linéarisables), sur ce genre de problème c'est assez simple : on passe par une méthode des moindres carrés.
Pour ce qui est du modèle (et de sa variante) que je dois étudier aujourd'hui je vous laisse apprécier :
sts = A * [1-exp(-B*str)] * [exp(C*str^2)] * (strt)^D
et
sts = A * [1-exp(-B*str)] * [1 + C*str + D*str^2] * (strt)^E
avec A, B, C, D les paramètres ajustables
sts la quantité observée expérimentalement
et str, strt mes variables expérimentales indépendantes
Je reste donc en manque d'idées concernant une méthode qui me permettrait d'approcher la résolution de ce problème. Je ne sais pas si les moindres carrés sont adaptés à ma démarche, et le cas échéant, je ne sais même pas quelle forme devrait prendre ma somme quadratique étant donné que je possède deux variables expérimentales ?
Merci d'avance :we:
Moindres carrés non linéaires
4 messages
- Page 1 sur 1
Salut,
A mon avis, que tu ait une, deux ou 36 variables expérimentales, ça ne change pas grand chose à la théorie :
Tu as des valeurs de départ_{1\leq i\leq n}) qui dans ton cas sont dans
qui dans ton cas sont dans 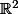 (str et strt), des valeurs d'arrivées
(str et strt), des valeurs d'arrivées _{1\leq i\leq n}) qui elles sont dans
qui elles sont dans  (sts) et une fonction
(sts) et une fonction  dépendant de multiples paramètres dont
dépendant de multiples paramètres dont 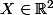 :
: ) (dans ton cas,
(dans ton cas, \in{\mathbb R}^4) . )
. )
Rq : tu est sûr que c'est le même D les deux fois dans ta deuxième formule ?
Après, la "méthode des moindres carrés", ça consiste à chercher le minimum de=\sum_{i=1}^n\big(y_i-f(\lambda,X_i)\big)^2\) en cherchant bien sûr le(s) point(s) critique(s) de la fonction, c'est à dire le(s) points où la différentielle est nulle (i.e. ou toutes les dérivées partielles sont nulles).
en cherchant bien sûr le(s) point(s) critique(s) de la fonction, c'est à dire le(s) points où la différentielle est nulle (i.e. ou toutes les dérivées partielles sont nulles).
Après, tout ça c'est bien beau, mais j'ai effectivement l'impression que, à part ton A, pour les autres composantes de il faille passer par du calcul numérique pour avoir les solutions...
il faille passer par du calcul numérique pour avoir les solutions...
A mon avis, que tu ait une, deux ou 36 variables expérimentales, ça ne change pas grand chose à la théorie :
Tu as des valeurs de départ
Rq : tu est sûr que c'est le même D les deux fois dans ta deuxième formule ?
Après, la "méthode des moindres carrés", ça consiste à chercher le minimum de
Après, tout ça c'est bien beau, mais j'ai effectivement l'impression que, à part ton A, pour les autres composantes de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
D'abord merci à vous deux d'avoir pris le temps de formuler une réponse. C'est très gentil et ça va m'aider.
Pour ce qui est de mapple je ne suis pas très bon avec et pour être honnête, je préfèrerais garder la main et programmer mon propre algorithme sur matlab. Il est même fort probable que ce sera plus simple pour moi :ptdr:
Ok Ben pour la fonction de minimisation, donc j'ai autant d'équations normales que de paramètres à fitter, je suis dans le coup ? Et pour répondre à ta question, oui, j'ai vérifié j'ai bien cinq paramètres A, B, C, D, E pour la deuxième formule.
Donc j'ai fait quelques recherches en plus et le problème est solvable par une méthode itérative qui fait appel à un développement de Taylor. Je dois pouvoir trouver une écriture matricielle au problème ce qui me permettrai de programmer un algorithme, jusque là tout est impec. Mais j'ai quand même une petite question : la solution étant itérative je dois donner une valeur initiale à mon vecteur des paramètres A B C D E et j'ai des biblios qui donnent des valeurs avec des ordres de grandeur très différents sur les paramètres de ma loi de comportement.
Je crains qu'une méthode de minimisation sur la dérivée (avec 5 paramètres !!!) ne donne pas de bons résultats si je n'ai pas un excellent vecteur de valeurs initiales de mes paramètres. Que je ne tombe que sur un minimum local de ma fonction de minimisation et donc un fit de mauvaise qualité...
Des idées sur cette question ?
Pour ce qui est de mapple je ne suis pas très bon avec et pour être honnête, je préfèrerais garder la main et programmer mon propre algorithme sur matlab. Il est même fort probable que ce sera plus simple pour moi :ptdr:
Ok Ben pour la fonction de minimisation, donc j'ai autant d'équations normales que de paramètres à fitter, je suis dans le coup ? Et pour répondre à ta question, oui, j'ai vérifié j'ai bien cinq paramètres A, B, C, D, E pour la deuxième formule.
Donc j'ai fait quelques recherches en plus et le problème est solvable par une méthode itérative qui fait appel à un développement de Taylor. Je dois pouvoir trouver une écriture matricielle au problème ce qui me permettrai de programmer un algorithme, jusque là tout est impec. Mais j'ai quand même une petite question : la solution étant itérative je dois donner une valeur initiale à mon vecteur des paramètres A B C D E et j'ai des biblios qui donnent des valeurs avec des ordres de grandeur très différents sur les paramètres de ma loi de comportement.
Je crains qu'une méthode de minimisation sur la dérivée (avec 5 paramètres !!!) ne donne pas de bons résultats si je n'ai pas un excellent vecteur de valeurs initiales de mes paramètres. Que je ne tombe que sur un minimum local de ma fonction de minimisation et donc un fit de mauvaise qualité...
Des idées sur cette question ?
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
