Approxiamtion, méthode des moindres carrés
31 messages
- Page 1 sur 2 - 1, 2
approxiamtion, méthode des moindres carrés
Bonjour,
Dans le cadre d'un cours d'analyse numérique j'ai un chapitre qui traite l'approximation de fonction et plus particulièrement la méthode des moindres carrés.
Malheureusement après plusieurs relecture du chapitre je n'arrive pas à comprendre la démarche à suivre. je comprend bien qu'il s'agit d'approximer au mieux une fonction mais il y a beaucoup de points que je ne saisi pas car je 'ai traité aucun exercice lors du cours.
J'ai cependant des énoncés d'exercices (sans la correction) et j'aimerai un peu d'aide pour résoudre le premier de la liste qui pourrait peut etre m'éclairer sur les suivants. je vous le cite:
Trouvez le meilleur polynome de degré 1, approximant la fonction réelle f définie sur l'intervalle [0,1] par f(x)=x²-2x+3 , au sens des moindres carrés.
voila, merci d'avance et bonne journée !
Dans le cadre d'un cours d'analyse numérique j'ai un chapitre qui traite l'approximation de fonction et plus particulièrement la méthode des moindres carrés.
Malheureusement après plusieurs relecture du chapitre je n'arrive pas à comprendre la démarche à suivre. je comprend bien qu'il s'agit d'approximer au mieux une fonction mais il y a beaucoup de points que je ne saisi pas car je 'ai traité aucun exercice lors du cours.
J'ai cependant des énoncés d'exercices (sans la correction) et j'aimerai un peu d'aide pour résoudre le premier de la liste qui pourrait peut etre m'éclairer sur les suivants. je vous le cite:
Trouvez le meilleur polynome de degré 1, approximant la fonction réelle f définie sur l'intervalle [0,1] par f(x)=x²-2x+3 , au sens des moindres carrés.
voila, merci d'avance et bonne journée !
D'accord mais comment déterminer les coefficient a et b ?
Je trouve mon cours pas clair du tout, et il n'y a pas de rapport avec la formule intégrale que tu m'a citée précédemment.
il est dit dans mon cours "le meilleur approximant g de f s'écrit g = ;) Ci.gi " puis " (f- ;)Cigi . gj)=0 " les sommes cités avant allant de i=1 à n et j=1,2,...,n
Cela abouti a une notation matricielle.
Je crois que dans le bout de mon cours que je t'ai cité, il faut déterminer le coeff C. aurait il un rapport avec les coeff a et b qu'li faut déterminer dans ta réponse?
j'espère avoir été clair...
Merci
Je trouve mon cours pas clair du tout, et il n'y a pas de rapport avec la formule intégrale que tu m'a citée précédemment.
il est dit dans mon cours "le meilleur approximant g de f s'écrit g = ;) Ci.gi " puis " (f- ;)Cigi . gj)=0 " les sommes cités avant allant de i=1 à n et j=1,2,...,n
Cela abouti a une notation matricielle.
Je crois que dans le bout de mon cours que je t'ai cité, il faut déterminer le coeff C. aurait il un rapport avec les coeff a et b qu'li faut déterminer dans ta réponse?
j'espère avoir été clair...
Merci
"le meilleur approximant g de f s'écrit g =Ci.gi " puis " (f-
Cigi . gj)=0
déjà, c'est quoi Ci, c'est quoi gi, c'est quoi f
Et ensuite, je suis cuiruex de savoir ce qui leur permet de dire que c'est le meilleur approximant.
Enfin, pour ce que je t'ai proposé, ca sert à rien de faire l'exo si tu comprends même pas ton cours. Lis wikipedia c'est mieux écrit.
la vie est une fête 
Bonjour,
Je vais vous donner mon explication de la méthodes des moindres carrés. Elle est surtout utilisée dans le cas de détermination d'un ensemble de valeurs à partir d'un ensemble d'observations en sur-nombre. Cela se traduit généralement par un système de M équations à N inconnues, M étant supérieur à N.
On démontre que la solution la plus probable d'un tel système est obtenue pour la valeur minimum de la somme des carrés des écarts constatés entre la valeur observée et la valeur calculée.
Ceci se traduit mathématiquement pas S=Somme(vi²) minimum
La fonction S est minimum si sa dérivée s'annule. Donc, on doit calculer les valeurs xi qui annulent S'.
S = Somme[0:1]((f(x)-(ax+b))²)
La déridée de S est la somme des dérivées partielles, c'est à dire
S' = Somme[0:1](dérivée de (f(x)-(ax+b))²) [la dérivée d'une somme est la somme des dérivées]
Maintenant, il suffit de résoudre; d'écrire que S' est = 0 et d'identifier les termes.
Je vais vous donner mon explication de la méthodes des moindres carrés. Elle est surtout utilisée dans le cas de détermination d'un ensemble de valeurs à partir d'un ensemble d'observations en sur-nombre. Cela se traduit généralement par un système de M équations à N inconnues, M étant supérieur à N.
On démontre que la solution la plus probable d'un tel système est obtenue pour la valeur minimum de la somme des carrés des écarts constatés entre la valeur observée et la valeur calculée.
Ceci se traduit mathématiquement pas S=Somme(vi²) minimum
La fonction S est minimum si sa dérivée s'annule. Donc, on doit calculer les valeurs xi qui annulent S'.
S = Somme[0:1]((f(x)-(ax+b))²)
La déridée de S est la somme des dérivées partielles, c'est à dire
S' = Somme[0:1](dérivée de (f(x)-(ax+b))²) [la dérivée d'une somme est la somme des dérivées]
Maintenant, il suffit de résoudre; d'écrire que S' est = 0 et d'identifier les termes.
Bonjour,
merci pour vos réponses, je suis allé lire le cour sur les moindre carrés sur wikipédia et cela m'a permis d'y voir un peu plus clair dans le cours (même s'il reste encore des zones de flous !).
Dlzlogic, j'ai essayer de suivre la méthode que tu m'a conseillé mais je crois que je l'ai mal appliqué car je ne trouve pas du tout le résultat voulu.
S est-il bien égale à la somme de i=0 à 1 ? parce que c'est ce que j'ai fait et j'obtiens S=(f(x0)-(ax0+b))²+(f(x1)-(ax1+b))²)
merci pour vos réponses, je suis allé lire le cour sur les moindre carrés sur wikipédia et cela m'a permis d'y voir un peu plus clair dans le cours (même s'il reste encore des zones de flous !).
Dlzlogic, j'ai essayer de suivre la méthode que tu m'a conseillé mais je crois que je l'ai mal appliqué car je ne trouve pas du tout le résultat voulu.
S est-il bien égale à la somme de i=0 à 1 ? parce que c'est ce que j'ai fait et j'obtiens S=(f(x0)-(ax0+b))²+(f(x1)-(ax1+b))²)
Oui c'est ce que je me suis dit aussi, il n'y a pas que 2 points sur [0;1] !
Mais pourquoi m'avez vous conseillé de minimiser l'intégrale entre 0 et 1 et Dlzogic affirme qu'il faut minimiser la somme entre 0 et 1 ?
Pourriez vous préciser un petit peu plus la marche à suivre, que jessaie de résoudre cette exercice?
Mais pourquoi m'avez vous conseillé de minimiser l'intégrale entre 0 et 1 et Dlzogic affirme qu'il faut minimiser la somme entre 0 et 1 ?
Pourriez vous préciser un petit peu plus la marche à suivre, que jessaie de résoudre cette exercice?
ben l'intégrale c'est un peu l'extension de la somme.
Dlzlogic te propose un exemple...
Si l'intégrale te gene, tu subdivises ton intervalles [0;1] en points de la forme k/n avec k=0 à n et tu fais tendre n vers l'infini, tu conserves alors ton expression de somme sous la forme
-(ax_k+b))^2)
où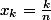
mais ca se rapporte également à l'intégrale proposée plus haut
edit: au facteur 1/n près...
edit2: après réflexion, je cherche une démo de la correspondance discret->continu
Dlzlogic te propose un exemple...
Si l'intégrale te gene, tu subdivises ton intervalles [0;1] en points de la forme k/n avec k=0 à n et tu fais tendre n vers l'infini, tu conserves alors ton expression de somme sous la forme
où
mais ca se rapporte également à l'intégrale proposée plus haut
edit: au facteur 1/n près...
edit2: après réflexion, je cherche une démo de la correspondance discret->continu
la vie est une fête 
ouais faut un peu suer mais ca va
[x²-2x+3 -(ax+b)]^2
(x^2 + x(-2-a) + 3-b )^2
[x^2+ x(-2-a)]^2 + (3-b)^2 + 2(x^2 + x(-2-a))(3-b)
ensuite on s'intéresse qu'aux termes dépendants de a et b (vu que de toute facon les constantes vont péter en dérivant par rapport à a ou b)
2x^3(-a) + x^2a^2 + b^2 -6b + 2(a(-3x) -b(x^2-2x) + ab(x)
ensuite tu primitives...et t'évalues en 1
-a/2 + a^3/3 + b^2 - 6b -3a -b(1/3-1) + ab/2
[x²-2x+3 -(ax+b)]^2
(x^2 + x(-2-a) + 3-b )^2
[x^2+ x(-2-a)]^2 + (3-b)^2 + 2(x^2 + x(-2-a))(3-b)
ensuite on s'intéresse qu'aux termes dépendants de a et b (vu que de toute facon les constantes vont péter en dérivant par rapport à a ou b)
2x^3(-a) + x^2a^2 + b^2 -6b + 2(a(-3x) -b(x^2-2x) + ab(x)
ensuite tu primitives...et t'évalues en 1
-a/2 + a^3/3 + b^2 - 6b -3a -b(1/3-1) + ab/2
la vie est une fête 
sigualex a écrit:d'accord et cela est aisé à calculer à la main ? parce que j'ai essayer toute vos méthodes et c'est super long de développer tous les carrés puis d'intégrer et de dériver pour trouver le minimum.
Je suis un peu désespéré, je comprend le but du chapitre mais vraiment pas les méthodes à appliquer.
Bonjour,
L'ai pas du être assez clair.
1- on démontre que la valeur chercher la plus probable est obtenue quand la somme des carrés est minimum. [je sais cela est controversé mais cela reste vrai pour l'immense majorité].
2- on ait qu'une fonction est minimum lorsque sa dérivée s"annule.
3- on écrit la somme des carrés
4- on écrit que la dérivée de cette somme de carrés doit être nulle.
5- la dérivée d'une somme est la somme des dérivées partielles.
6- on discrétise la fonction
Donc on a S' = Somme((f(x) - (ax+b))²)')
On peut l'écrire pour 0.1 à 0.9 avec on pas de 0.1
Mais, sauf faute dans ma tête, on doit réussir à avoir des termes de la forme n(quelque-chose), ce qui implique que le choix de n devrait être sans influence.
Il ne faut naturellement pas développer les carrés.
J'ai essayé de résoudre algébriquement votre problème, j'y suis pas arrivé.
Comme je vous l'ai dit lors de ma première réponse, la méthode des moindres carrés n'est pas vraiment utilisée dans ce contexte.
Alors, j'ai calculé la valeur des différents y pour les valeurs de x de 0 à 1 avec un pas de 0.1, et j'ai calculé la régression linéaire.
Comme je vous l'ai dit lors de ma première réponse, la méthode des moindres carrés n'est pas vraiment utilisée dans ce contexte.
Alors, j'ai calculé la valeur des différents y pour les valeurs de x de 0 à 1 avec un pas de 0.1, et j'ai calculé la régression linéaire.
Bonsoir, j'ai un peu de mal à comprendre pourquoi vous voulez discrétiser un problème qui est fondamentalement continu. Ce que fatal_error a dit au tout début est la bonne démarche, et on peut résoudre ça de façon géométrique (je pense que c'est cette façon de faire que l'énoncé attend puisque sigulaex parle de matrices, mais sinon on peut aussi faire en minimisant l'intégrale considérée comme une fonction de deux variables) : il s'agit de calculer, dans l'espace euclidien des polynômes de degré au plus 2 muni du produit scalaire =\int_0^1 P(x)Q(x)dx) , le projeté orthogonal de X²-2X+3 sur le plan formé par les polynômes de degré au plus 1. On peut déterminer le supplémentaire orthogonal de ce plan. On trouve - sauf erreur de calcul - que ce supplémentaire est la droite engendrée par X²-X+1/6, ce qui mène à la réponse. Au final, la fonction recherchée est x -> -x + 17/6.
, le projeté orthogonal de X²-2X+3 sur le plan formé par les polynômes de degré au plus 1. On peut déterminer le supplémentaire orthogonal de ce plan. On trouve - sauf erreur de calcul - que ce supplémentaire est la droite engendrée par X²-X+1/6, ce qui mène à la réponse. Au final, la fonction recherchée est x -> -x + 17/6.
Comme d'habitude, tes propos ne veulent rien dire... Et arrête de parler de cette "immense majorité" qui n'inclut pas grand-monde à part toi.
Dlzlogic a écrit:1- on démontre que la valeur chercher la plus probable est obtenue quand la somme des carrés est minimum. [je sais cela est controversé mais cela reste vrai pour l'immense majorité].
Comme d'habitude, tes propos ne veulent rien dire... Et arrête de parler de cette "immense majorité" qui n'inclut pas grand-monde à part toi.
Bonjour Skullkid,
Pour la valeur 17/6, je suis d'accord, mais dans le cadre de la discussion dont le titre est "approximation, ...", moi, je propose 2.85.
D'autre part, un grand intérêt de la méthode des moindres carrés consiste dans le fait que pour rendre minimum la somme des carré, on annule sa dérivée. Je n'ai pas vu que tu aies fait cela.
Et toi, qu'est-ce que tu proposes comme méthode pour trouver la valeur la plus probable ?
Pour la valeur 17/6, je suis d'accord, mais dans le cadre de la discussion dont le titre est "approximation, ...", moi, je propose 2.85.
D'autre part, un grand intérêt de la méthode des moindres carrés consiste dans le fait que pour rendre minimum la somme des carré, on annule sa dérivée. Je n'ai pas vu que tu aies fait cela.
Et toi, qu'est-ce que tu proposes comme méthode pour trouver la valeur la plus probable ?
sigualex a écrit:Merci beaucoup pour vos réponses !
J'ai trouvé a=-1 et b=17/6 avec la méthode de fatal error ce qui confirme le résultat de Skulki.
Par contre je n'arrive pas à comprendre comment tu as procédé pour trouver ce résultat Skullkid... comment as tu trouvé le supplémentaire orthogonal au plan?
Tu prends la base (1,x,x^2) et tu orthogonalises par gram-schmidt ta base, sous le produit scalaire indiqué par Skullkid.
Tu as alors, par exemple, la base (1, x-1/2 , x^2 -x + 1/6) comme base orthonormale sous le produit scalaire indiqué.
Les deux premiers vecteurs de bases engendrent le plan des polynômes de degré au plus 1. Le 3ème vecteur de base y est orthogonal par construction (car orthogonal au 1er et au 2è vecteurs de base), donc il est le supplémentaire orthogonal du plan des polynômes de degrés au plus 1.
Puisque tu peux décomposer ton vecteur x^2 - 2x + 3 en un vecteur qui est dans le plan (la projection) plus le vecteur qui y est orthogonal, tu as
v = proj + orth => v - orth = proj
Donc x^2 - 2x + 3 - x^2 + x - 1/6 = -x + 17/6
Je comprend le but de la méthode mais je n'arrive pas à comprendre comment tu a trouvé ta base orthonormale.
Tout d'abord tu prend la base (1,x,x^2) car mon polynôme est de degré 2 ? s'il avait été de degré 3 tu arais pris la base (1,x,x^2,x^3) ??
Ensuite je n'arrive pas à l'orthogonaliser par Gram-Schmidt et à obtenir la base (1,x-1/2,x^2-x+1/6)
Tout d'abord tu prend la base (1,x,x^2) car mon polynôme est de degré 2 ? s'il avait été de degré 3 tu arais pris la base (1,x,x^2,x^3) ??
Ensuite je n'arrive pas à l'orthogonaliser par Gram-Schmidt et à obtenir la base (1,x-1/2,x^2-x+1/6)
sigualex a écrit:Je comprend le but de la méthode mais je n'arrive pas à comprendre comment tu a trouvé ta base orthonormale.
Tout d'abord tu prend la base (1,x,x^2) car mon polynôme est de degré 2 ? s'il avait été de degré 3 tu arais pris la base (1,x,x^2,x^3) ??
Ensuite je n'arrive pas à l'orthogonaliser par Gram-Schmidt et à obtenir la base (1,x-1/2,x^2-x+1/6)
Oui, le sous-espace des polynômes de degrés 2, puisque l'on veut projeter un polynôme de degré 2 sur un polynôme de degré 1.
Soit (o1,o2,o3) la base orthonormale que l'on veut acquérir à partir de (1,x,x^2) := (e1,e2,e3) muni du produit scalaire
Tu initialises :
o1 = e1
-> o1 = 1
Là, t'as enlevé à e2 la partie projetée sur o1, donc il y est maintenant orthogonal.
Trouve o3
31 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
