Methode des differences finies et divisées

par **jeremy58** » 24 Avr 2007, 15:38

Bonjour,
J'ai un exercice qui fait appel aux methodes des differences finies et divisées, mais je ne vois pas ce que c'est!
Il faut calculer le polynome d'interpolation de lagrange de la fonction
1
f(x)= --------- aux points -1,0,1,2
1 + x²
par ces 2 méthodes!
merci

par **Joker62** » 24 Avr 2007, 16:09

Si je ne m'abuse, les différences divisées, c'est pour exprimer l'interpolant dans la base de Newton...

par **jeremy58** » 27 Avr 2007, 08:32

merci de m'avoir aider, la methode des differences divisées est une methode de newton. Je suis donc arrivé à trouver le polynome par la methode des differences divisées mais mon soucis c'est que je ne trouve pas la meme chose que par la methode de lagrange, est-ce normal?
Par contre, je ne vois comment il faut faire par la methode des differences finies?
Pourriez-vous m'aider?
Merci

par **jeremy58** » 27 Avr 2007, 21:03

N'ayant pas de reponse je me permet de relancer mon sujet.
Merci

par **jeremy58** » 30 Avr 2007, 22:03

Bonsoir,
je suis désolé de relancer de nouveau le sujet mais je suis toujours coincé!
Merci

par **alben** » 30 Avr 2007, 23:44

Bonsoir,

Je peux te confirmer que les deux interpolations donnent le même polynôme.
Si tu ne donnes pas les polynômes auxquels tu es arrivé, on ne pourra pas te dire là où ça dérape
(essaie d'utiliser latex et en tout cas évite les présentations artistiques de fractions comme dans ton premier post)

par **jeremy58** » 01 Mai 2007, 09:26

par la methode de lagrange, je trouve :

par la methode des differences divisées, je trouve :

par **alben** » 01 Mai 2007, 09:59

Bonjour,

Avec Lagrange tu brules, il n'y a que ton coeff en

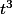
qui ne va pas
Avec Newton, tu en es loin. Qu'est-ce que tu a obtenu comme coeff des polynomes de base ?
J'ai 0,5 0,5 -0.5 0.2

par **jeremy58** » 01 Mai 2007, 10:18

je dois avoir une erreur sur le dernier, j'ai :
0,5 0,5 -0,5 -0,1

par **alben** » 01 Mai 2007, 10:35

tu as bien f(2)=0,2 ?
Ca pourrait expliquer ton pb

par **jeremy58** » 01 Mai 2007, 11:26

je trouve maintenant par la methode de lagrange :

et je trouve la meme chose par la methode des differences divisés.
Il ne me reste plus qu'a finir la methode des differences finies.
Merci

par **jeremy58** » 01 Mai 2007, 11:37

c'est bon je trouve le bon resultat aussi avec la methode des differnces finies
Merci beaucoup de m'avoir aider

Methode des differences finies et divisées

methode des differences finies et divisées

Qui est en ligne