Différences divisées - Exercice

[Phoenix944]

Bonjour,

J'ai un exercice sur les différences divisées qui me résiste depuis longtemps. L'énoncé est :

On considère une subdivision régulière {x0, . . . , xn} de l'intervalle [a, b] avec x0 = a, xk = x0 + kx et x = (b a)/n.

1) Calculer les différences divisées suivantes : f[x0], f[x0, x1], f[x0, x1, x2] et f[x0, x1, x2, x3].
>>> Il suffit juste d'appliquer une formule, pas bien compliqué je l'ai fais.

2) Montrer par récurrence que :


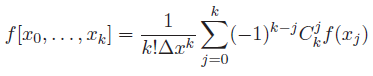
C'est la deuxième question qui me pose beaucoup de soucis, j'apprécierai un petit coup de pouce

Merci d'avance.

[savancosinus]

Bonjour,

je ne sais pas précisément où tu bloques ... mais écrivons le début :

Déjà on suppose que la formule que tu as écrite est ton hypothèse de récurrence.
Ensuite le cas k + 1 s'écrit :



Là on utilise l'hypothèse de récurrence pour écrire :


et


je te laisse faire la suite, ça ressemble énormément à la démonstration de la formule du binôme de Newton, à savoir :
Manipuler les indices de somme pour transformer le terme en puis regrouper tous les termes dans une même somme en utilisant une relation entre les coefficients binomiaux.

Bon courage.

[Phoenix944]

Bonjour,

D'accord, tu m'as donné un bon point de départ, je vais continuer à travailler là dessus. Merci pour le coup de main.

A bientôt.