Bonjour, je suis tombé sur cet exo:
Soit

un espace métrique compact (par exemple une partie compacte de

), soit
)
la

-algèbre borélienne de

et soit

une mesure finie sur

.
Montrer que

est régulière, c'est à dire que pour tout
)
, on a
 = \sup\ \{\mu(K):\ K\subset B \mbox{ et } K \mbox{ compact}\} = \inf\ \{\mu(U):\ B\subset U \mbox{ et } U \mbox{ ouvert}\})
.
Indication: On pourra considérer l'ensemble

des
)
tels que, pour tout

, il existe

compact et

ouvert vérifiant
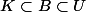
et
 < \varepsilon)
, et montrer que

contient au moins les ouverts.
J'ai du mal à voir pourquoi l'ensemble vide est compact. La partie vide est compacte si elle est séparée et si de tout recouvrement ouvert de

on peut extraire un sous-recouvrement fini de

.
Le seul recouvrement de

est
 = \{\emptyset\})
qui est fini.
Mais je ne vois pas comment montrer que

est séparé.
Après pour la résolution de l'exercice je crois que j'ai trouvé un plan:
1) montrer que les ouverts de

sont dans

;
2) montrer que

est une

-algèbre, et donc on a
 \subset \mathcal{A})
.
J'introduis les notations :
:\ K\subset B \mbox{ et } K \mbox{ compact}\})
, et
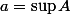
;
:\ B\subset U \mbox{ et } U \mbox{ ouvert}\})
, et
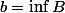
.
Par la croissance (au sens de l'inclusion) de la mesure

, il est clair que
 \leq b)
. Il reste à montrer que
 \geq b)
.
Ensuite, soit un entier

. Il existe un compact
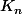
et

tel que
[CENTER]
 < 1/n)
et
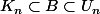
.[/CENTER]
D'où
 < 1/n)
et
 < 1/n)
.
Autrement dit
-\mu(B) < 1/n)
et
-\mu(K_n) < 1/n)
.
Donc
)_n)
est une suite de

et
)_n)
est une suite de

, les deux ayant pour limite
)
. Donc
 \geq b)
.
