Espace metrique est connexe, compact et complet
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 25 Mai 2017, 20:58
par ArtyB » 25 Mai 2017, 20:58
Bonjour,
Je connais les définitions des espaces complets; compacts et connexes, mais dans la pratique comment déterminer simplement si un espace est complexe, compact ou connexe ?
Prenons par exemple l'espace metrique suivant:
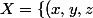 \in \R ^3 , x^2+y^2+z^2=1\})
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 25 Mai 2017, 21:11
par pascal16 » 25 Mai 2017, 21:11
Les définitions topologiques valables partout sont aussi les plus compliquées à vérifier.
Les définitions analytiques applicables dans ce genre sont souvent plus facile à démontrer.
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 25 Mai 2017, 21:24
par ArtyB » 25 Mai 2017, 21:24
C'est à dire ?
Je me lance:
1/ Compacité: on montre que X est fermé et borné donc compact.
2/ Completude: comment montrer que toute suite de Cauchy est covnergente dans X ?
3/ Connexité: comment montrer que pour tout élément g=(x,y,z) de X il existe une suite qui converge vers g ?

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 25 Mai 2017, 23:30
par Lostounet » 25 Mai 2017, 23:30
ArtyB a écrit:C'est à dire ?
Je me lance:
1/ Compacité: on montre que X est fermé et borné donc compact.
2/ Completude: comment montrer que toute suite de Cauchy est covnergente dans X ?
3/ Connexité: comment montrer que pour tout élément g=(x,y,z) de X il existe une suite qui converge vers g ?
Dans ton 1/, tu dois mentionner le fait que tu travailles dans R^3 qui est de dimension finie: c'est ce qui te permet de t'en sortir si facilement avec "fermé borné" <=> "compact".
Concernant ta complétude, une fois tu as montré que c'est un fermé, c'est fini: Si (E;d) est un espace métrique complet et que F est un fermé de E, alors F complet.
3/ Concernant ta connexité, tu peux utiliser la connexité par arcs par exemple (connexe par arcs implique connexe): tu peux directement trouver un moyen de relier deux points a et b de la sphère par un certain paramétrage continu.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 26 Mai 2017, 06:58
par ArtyB » 26 Mai 2017, 06:58
Merci beaucoup.
1/ En effet, je viens de voir que si l'on se dans un ensemble infini alors le fait que X soit fermé et borné n'implique pas qu'il est compact.
2/ Oui mais il faut montrer que E est complet d'abord.... et comment faire ça ?
3/ Je crois que je vois mais comment trouver un chemin reliant deux points g=(x,y,z) et g'=x'y',z') dans X ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 26 Mai 2017, 09:05
par zygomatique » 26 Mai 2017, 09:05
ArtyB a écrit:Bonjour,
Je connais les définitions des espaces complets; compacts et connexes, mais dans la pratique comment déterminer simplement si un espace est
complexe, compact ou connexe ?
Prenons par exemple l'espace metrique suivant:
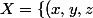 \in \R ^3 , x^2+y^2+z^2=1\})
c'est quoi un espace
complexe ?
soit f la fonction définie par ::
 = x^2 + y^2 + z^2)
f est continue et {1} est fermé donc
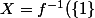)
est fermé
X est évidemment borné puisque
 \in X \iff |x| \le 1 \ et \ |y| \le 1 \ et \ |z| \le 1})
conclusion ?
as-tu reconnu en X la sphère unité de R^3 ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 26 Mai 2017, 17:30
par Lostounet » 26 Mai 2017, 17:30
ArtyB a écrit:2/ Oui mais il faut montrer que E est complet d'abord.... et comment faire ça ?
3/ Je crois que je vois mais comment trouver un chemin reliant deux points g=(x,y,z) et g'=x'y',z') dans X ?
As-tu un cours sur les espaces complets?
De quoi veux-tu partir? Tu veux redémontrer la complétude de E= R^3 ...? C'est dans tous les cours... c'est un peu un truc de base (je veux pas dire que c'est si évident, simplement que quand on veut travailler sur des espaces fonctionnels plus difficiles, j'utilise la complétude de R ou de C (voire de
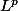
pour la norme convenable mais cette complétude est difficile à prouver: c'est le théorème de Riesz Fischer) que je suppose acquise...).
J'ai constaté qu'on s'appuie toujours sur la complétude de quelqu'un (il faut préciser pour quelle norme en dimension infinie) pour prouver que quelqu'un est complet.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 26 Mai 2017, 20:28
par pascal16 » 26 Mai 2017, 20:28
Une hyperboloïde à 2 nappes demanderait un peu plus de réflexion
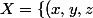 \in \R ^3 , x^2+y^2-z^2=-1\})
(pas connexe, pas borné, complet, fermé ?)
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 26 Mai 2017, 23:57
par ArtyB » 26 Mai 2017, 23:57
@Zygomatique
"complet" mea culpa.
J'avais reconnu la sphère de

qui est bornée et fermée donc compacte. Mais ce sont les arguments démontrant borné + fermé = compact qui m'intéressaient surtout.
@Lostounet
Merci. Non pas besoin de redémontrer la complétude de

mais c'est plus la méthodologie qui permet d'appliquer les propriétés vues en cours qui m'intéressent. Par exemple ici comme {1} est fermé et f continue, alors
=X)
est fermé.
Et ici comment utiliser la connexité par arcs ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités