Mesure de comptage !
59 messages
- Page 1 sur 3 - 1, 2, 3
mesure de comptage !
Bonjour :
Est ce que vous pouvez me rappeler de l'expression de la mesure de comptage ?!
Merci d'avance !!
Est ce que vous pouvez me rappeler de l'expression de la mesure de comptage ?!
Merci d'avance !!
Salut "B_J" :
Une autre petite question :
Est ce que l'integrale de la fonction nulle est égale à la fonction constante ou bien fonction nulle !!
La derivée de la fonction constante est égale à la fonctio nulle donc l'integrale de la fonction nulle est égale à la fonction constante , c'est ça ?
Merci d'avance !!
Une autre petite question :
Est ce que l'integrale de la fonction nulle est égale à la fonction constante ou bien fonction nulle !!
La derivée de la fonction constante est égale à la fonctio nulle donc l'integrale de la fonction nulle est égale à la fonction constante , c'est ça ?
Merci d'avance !!
Bonsoir :
"Joker" , je crois pas que ce que tu as dit est correcte :
Dans un cours de theorie de la mesure j'ai trouvé ce qui suit :
Pour mesurable positive :
mesurable positive :
 presque partout.
presque partout.
Demonstration :
On suppose presque partout, on a alors :
presque partout, on a alors :  ... etc.
... etc.
Donc :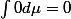 et non pas
et non pas 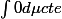 comme tu m'as dit ... ? ou est la difference ... ?!
comme tu m'as dit ... ? ou est la difference ... ?!
Si quelqu'un a une idée, merci de la poster sur le coup !!
Merci d'avance !!
"Joker" , je crois pas que ce que tu as dit est correcte :
Dans un cours de theorie de la mesure j'ai trouvé ce qui suit :
Pour
Demonstration :
On suppose
Donc :
Si quelqu'un a une idée, merci de la poster sur le coup !!
Merci d'avance !!
Bonsoir Barbu,
une intégrale est un scalaire par définition et non une fonction.
L'intégrale de la fonction nulle est nulle:
on peut voir la fonction nulle comme une fonction en escalier.
Et donc son intégrale est facile à calculer, c'est 0.
Est ce que l'integrale de la fonction nulle est égale à la fonction constante ou bien fonction nulle !!
une intégrale est un scalaire par définition et non une fonction.
L'intégrale de la fonction nulle est nulle:
on peut voir la fonction nulle comme une fonction en escalier.
Et donc son intégrale est facile à calculer, c'est 0.
barbu23 a écrit:Je dors pas bien ces derniers temps !! :lol2:
D'accord !! merci "legeniedesalpages" !!
Maispar rapport à quelle partie de
.. C'est à dire : pour n'importe quel
mesurable dans
:
... c'est une convention, ou bien elle se calcule !!
Et désolé pour ces betes questions ... ! :lol2:
Par rapport à n'importe quelle partie mesurable
Notons
tu as
Et de plus il est immédiat que
Donc
Attention l'intégrale de lebesgue est plus générale:
 .
.
On peut plus écrire cette notation avec les crochets, car justement, les boréliens ne sont plus forcément des intervalles. Par exemple si tu prends l'ensemble .
.
Si tu prends une "primitive" F d'une fonction f, (en supposant qu'elle existe) et que tu fais et que tu fais-F(inf A)) , on voit bien que tu vas compter un gros morceau d'aire en trop.
, on voit bien que tu vas compter un gros morceau d'aire en trop.
On peut plus écrire cette notation avec les crochets, car justement, les boréliens ne sont plus forcément des intervalles. Par exemple si tu prends l'ensemble
Si tu prends une "primitive" F d'une fonction f, (en supposant qu'elle existe) et que tu fais et que tu fais
barbu23 a écrit:Salut : "ThSQ" :
Pour les fonctions continues c'est toujours verifiée, mais pour la classe des fonctions mesurables il y'a certains fonctions qui ne verifient pas cette equivalences ... C'est ça ?!!
Et on a toujours :.
Merci d'avance !!
C'est vérifiée pour les fonctions qui ne sont pas nulles presques partout,
et par contre si tu prends par exemple
59 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
